 01.字节秋招高频算法汇总
01.字节秋招高频算法汇总
# 作者
# 字节秋招高频算法汇总
接下来讲一下 字节秋招 中的高频算法题,分为三个部分: 基础篇 、 中级篇 、 进阶篇
目的就是为了应对秋招中的算法题,其实过算法题的诀窍就在于 理解的基础上 + 背会
看到一个题目,首先要了解题目考察的算法是什么,这个算法要理解,至于具体实现的话,就靠背会了(多写、多练),没有什么捷径,可以 尝试一个题目手写 3-5 遍 ,加强一下记忆!
还有一点要注意的是,在大厂的笔试中, 可能考察算法的方式是 ACM 模式 ,这一点和力扣上不同,ACM 模式需要我们自己去引入对应的包,以及自己写算法,力扣是将方法框架给定,只需要在方法内写代码就可以了,这一点要注意!
大厂高频算法题汇总文章目录:
# 基础篇
字节的算法题相对于阿里来说更加丰富一些,之前在阿里的算法题中是没有包含 快速查找 、二分查找 的题目的,所以这里可以重点看一下,考察算法有:
- 贪心
- DFS 、 BFS :使用 DFS 搜索树、反转字符串、BFS 遍历节点、DFS 返回二叉树右视图
- 双指针
- 快速排序
- 二分查找

# LC 455. 分发饼干(简单)
题目描述:
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
这道题目是典型的 贪心 问题
题目要求 饼干尺寸 > 孩子的胃口 才可以满足孩子,那么可以对 饼干尺寸 、孩子的胃口 都 从小到大 进行排序
贪心来做 的话,将小饼干优先分给胃口小的孩子,这样可以将尺寸大的饼干留在后边给更大胃口的孩子吃
证明这个 贪心算法 正确性的话,可以这么想,如果将一个较大的饼干分给这个胃口较小的孩子,那么为什么不将一个较小的饼干分给这个胃口较小的孩子?显然先分配较小的饼干,可以将大饼干留给后边胃口较大的孩子, 这样既可以满足这个胃口较小的孩子,也可以更大几率满足后边胃口较大的孩子
贪心类的问题虽然看着很简单,但是要证明我们这样贪心去做是正确的比较难,因此看到一个题目发现像贪心题,可以先尝试贪心做一下,如果通过不了,说明贪心不是正解,再尝试其他方法
代码如下 :
class Solution {
public int findContentChildren(int[] g, int[] s) {
// 对饼干、孩子的胃口进行排序
Arrays.sort(g);
Arrays.sort(s);
int n = g.length;
int m = s.length;
// 记录结果
int res = 0;
// 记录遍历的孩子的下标
int idx = 0;
// 遍历饼干
for (int i = 0; i < m; i ++) {
// 如果第 i 个饼干可以喂饱第 idx 个孩子,就将结果 + 1
if (idx < n && g[idx] <= s[i]) {
res ++;
idx ++;
}
}
return res;
}
}
# LC 199. 二叉树的右视图(中等)
题目描述:
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
这道题目需要拿到二叉树的 右视图 ,也就是右边的第一个节点,不过要注意右边的第一个节点不一定是右节点,也有可能右节点为空,那么就是左节点了,如下:

那么解题思路的话,有两种 dfs 或者 bfs
# DFS 解决
先说 dfs 解决的思路,可以按照 根节点 -> 右节点 -> 左节点 的顺序进行遍历
由于每一层我们只需要加最右边的节点,但是遍历的话,会遍历这一层的多个节点
因此通过一个 depth 变量来记录遍历的深度,由于每一层都会添加一个节点,这里假设节点放在 res 数组中了,那么如果 depth == res ,说明上一层刚遍历完,现在遍历的是新的一层的第一个节点,我们定义的递归顺序就是先便利右节点,因此一定会先遍历 右视图 的节点,将该节点加入 res 中即可
代码如下 :
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> rightSideView(TreeNode root) {
dfs(root, 0);
return res;
}
public boolean dfs(TreeNode root, int depth) {
// 设置递归终止条件
if (root == null) {
return false;
}
// 如果当前遍历的节点的新的一层的第一个节点
if (depth == res.size()) {
res.add(root.val);
}
// 先遍历右节点,深度 + 1
dfs(root.right, depth + 1);
// 再遍历左节点,深度 + 1
dfs(root.left, depth + 1);
return true;
}
}
# BFS 解决
BFS 来解决的话,可以将每一层的节点加入到队列中,先加入左节点,再加入右节点,那么队列中的最后一个元素肯定就是 右视图 了,加入到结果集中即可
代码如下 :
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> res = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
public List<Integer> rightSideView(TreeNode root) {
// 如果根节点是空的话,就直接返回就好了
if (root == null) return res;
// 先将根节点加入,进行 bfs
queue.offer(root);
while (!queue.isEmpty()) {
// 计算队列中元素的数量 size,这些元素都是同一层的节点,对他们进行遍历,拿到下一层的节点
int size = queue.size();
for (int i = 0; i < size; i ++) {
// 弹出元素,加入左、右子节点
TreeNode cur = queue.poll();
// 如果左、右节点不为空的话,就加入队列
if (cur.left != null) queue.offer(cur.left);
if (cur.right != null) queue.offer(cur.right);
// 如果是当前队列的最后一个节点,就是右视图的节点,加入结果中
if (i == (size - 1)) {
res.add(cur.val);
}
}
}
return res;
}
}
# LC 169. 多数元素(简单)
题目描述:
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
输入:nums = [3,2,3]
输出:3
这道题目要找出数组中的多数元素,最简单的解题思路 就是直接对 nums 数组进行排序,那么这个多数元素一定在数组中间的位置,也就是 [n/2] 的位置
还有一个思路就是 摩尔投票法思路 :先初始化一个候选人 candidate ,这个候选人默认为 nums[0] ,初始化一个投票数 count 为 1,那么每当碰到相同的数,就将 count + 1 ,碰到不同的数,就将 count - 1 ,如果 count 减为 0 之后,就更换候选人,并将票数 count 置为 1
这样子由于数组中一定有一个 多数元素 ,这个多数元素和其他元素抵消,最后一定会剩余一个 多数元素 ,作为候选者返回即可!
直接排序做的话,时间复杂度是 O(NlogN) ,使用摩尔投票法做的话,时间复杂度是 O(N)
这里写一下 摩尔投票法 的代码:
class Solution {
public int majorityElement(int[] nums) {
// 初始化候选者、票数
int candidate = nums[0];
int count = 1;
for (int i = 1; i < nums.length; i ++) {
// 如果相同就 + 1
if (nums[i] == candidate) {
count ++;
} else {
// 否则就 -1
count --;
}
// 如果票数为 0,就更换候选者
if (count == 0) {
count = 1;
candidate = nums[i];
}
}
return candidate;
}
}
# LC 215. 数组中的第K个最大元素(中等)
题目描述:
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
输入: [3,2,1,5,6,4], k = 2
输出: 5
这道题目可以看作是一个模板题目了,选择数组中第 K 大的元素
可以借助快速排序的模板来做,快速排序的话是先将数组分为两段,一段 <=x,另一端 >=x,再对每一段继续递归分段进行排序,过程如下:
先找到数组中的一个数,定义为 x ,之后开始循环:从左边开始遍历找到第一个大于 x 的数,从右边开始遍历找到第一个小于 x 的数,将这两个数进行互换,直到 左右指针碰撞 ,则此时整个数组被分为 <= x 和 >= x 的两段区间,如下:

由于快排是从小到大进行排序,所以这里我们先假设 要找第 k 小的数 ,那么就判断 第 k 小的数 左边区间还是右边区间,之后再遍历指定区间找到第 k 小的数即可
题目中要求找 第 k 大 的数,但是我们实现的算法找的是 第 k 小 的数,因此可以令 k = (n-k+1) ,这样题目要求找第 k 大的数就转换为了找第 k 小的数
这道题目和快速排序一样,都是较常见的模板题,可以将代码直接背了
代码如下:
class Solution {
public int findKthLargest(int[] q, int k) {
int n = q.length;
// 题目要求找第 k 大的数,也就是第 n-k+1 小的数,我们的算法是找第 k 小的数,所以这里转化一下
return quickSelector(q, 0, n - 1, n-k+1);
}
// 找到第 k 小的数
public int quickSelector(int[] q, int l, int r, int k) {
// 如果左右指针碰撞,就返回 q[l]
if (l >= r) return q[l];
// 定义左右指针,定义 x 为数组中间的位置,遍历数组,将数组分为 <=x 和 >=x 的两段区间
// (l + r) >> 1 表示右移一位,也就是除以 2
int i = l - 1, j = r + 1, x = q[(l + r) >> 1];
while (i < j) {
do i ++; while(q[i] < x);
do j --; while(q[j] > x);
// 开始交换元素
if (i < j) {
int tmp = q[i];
q[i] = q[j];
q[j] = tmp;
}
}
// 如果左边区间长度大于 k,那么第 k 小的数就在左边区间
if ((j-l+1) >= k) return quickSelector(q, l, j, k);
// 否则,在右边区间,将 k 减去左边区间的长度即可(左边区间的数全都小于右边区间的数)
else return quickSelector(q, j + 1, r, k - (j-l+1));
}
}
# LC 103. 二叉树的锯齿形层序遍历(中等)
题目描述:
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
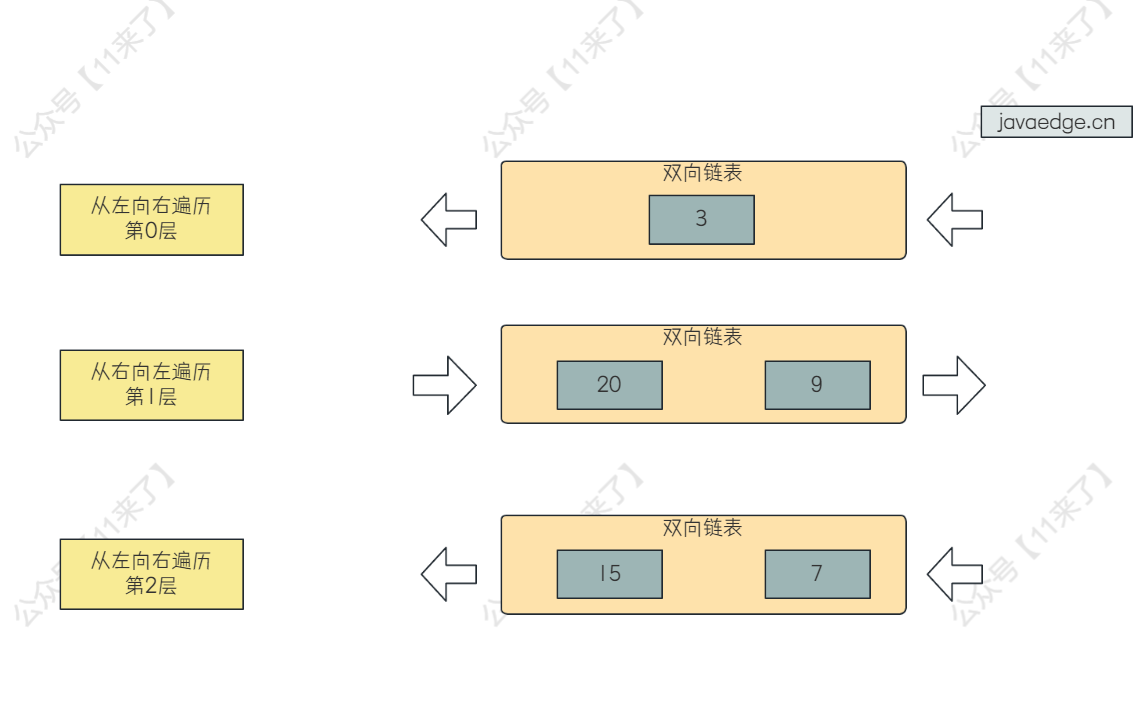
这道题目就是一层从左向右遍历,下一层从右向左遍历,交替进行即可
那么我们只需要记录 已经遍历的层数 depth ,就可以知道当前这一层是以什么顺序遍历了
使用 BFS 来做,先遍历左子树、再遍历右子树,只不过在记录结果的时候:
- 如果是 从左向右 遍历的话,就将节点值加入到双向链表的最后
- 如果是 从右向左 遍历的话,就将节点值加入到双向链表的最前
按题目中给的节点,遍历流程如下:
代码如下:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
// 判空
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int n = queue.size();
// 已经遍历的二叉树深度
// 如果 depth 是偶数,从左到右遍历
// 如果 depth 是奇数,从右到左遍历
int depth = res.size();
LinkedList<Integer> tmp = new LinkedList<>();
for (int i = 0; i < n; i ++) {
TreeNode cur = queue.poll();
// 从左到右遍历
if (depth % 2 == 0) tmp.addLast(cur.val);
// 从右到左遍历
else tmp.addFirst(cur.val);
if (cur.left != null) queue.offer(cur.left);
if (cur.right != null) queue.offer(cur.right);
}
res.add(tmp);
}
return res;
}
}
# LC 33. 搜索旋转排序数组(中等)
题目描述:
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
二分查找只能在有序数组中查找 ,这道题目中的数组并不是有序的,不能直接通过 二分 来解决,因此要想办法将数组变为有序的,再使用 二分解决
数组是按照某一个节点进行旋转了,因此数组是分为了两个有序区间的,那么我们只需要判断 target 和 nums[0] 的值就可以判断目标值在哪一个有序区间了:
- 如果 target >= nums[0] ,那么目标值在左边有序区间
- 如果 target < nums[0] ,那么目标值在右边有序区间
知道目标值在哪个区间了,就可以在该区间内进行二分查找了
代码如下:
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
// 先二分,找出来第一个区间中最大值,也就是第一个区间的右端点
int l = 0, r = n - 1;
while (l < r) {
// 如果 r = mid-1,这里要 mid = l + r + 1 >>1
// 如果 r = mid,这里要 mid = l + r >> 1
int mid = l + r + 1 >> 1;
if (nums[mid] >= nums[0]) l = mid;
else r = mid - 1;
}
// 此时 l 和 r 就是左边区间的右端点
// 如果需要找的值在左边区间,就将二分区间设置为[0, r]
if (target >= nums[0]) l = 0;
// 如果需要找的值在右边区间,就将二分区间设置为[l+1, n-1]
else {
l ++;
r = n - 1;
}
// 开始二分查找目标值
while (l < r) {
int mid = l + r + 1 >> 1;
// 如果当前 mid 节点 <=target,说明 target 值在右边,令 l=mid
if (nums[mid] <= target) l = mid;
// 如果当前 mid 节点 >target,说明 target 值在左边,令 r=mid-1
else r = mid - 1;
}
// 这里判断使用 r 而不是 l
//是因为 如果数组中只有 1 个值,上边两个二分都不会走,如果走到 if 条件中执行了 l++,就会导致数组越界
if (nums[r] == target) return l;
return -1;
}
}
# 中级篇
字节高频算法,在中等篇主要考察 思维 、时间复杂度的优化 、DFS 、矩阵相邻格子移动 、全排列 ,如下:

# LC 15. 三数之和(中等)
题目描述:
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。
请你返回所有和为 0 且不重复的三元组。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
**注意:**答案中不可以包含重复的三元组。
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
这道题目给出的 数组长度 最大是 3000,那么如果我们去暴力做的话,需要定义 3 个指针,时间复杂度为 O(N^3^) ,肯定会超时
(一般在算法题中认为 1s 可以执行 10^8^ 次的运算,如果超过就会导致超时)
那么我们必须将时间控制到 O(N^2^) 以内
优化思路 为:
先对数组排序,保证数组有序
先枚举指针 i ,对于确定的指针 i,再枚举另外两个指针 l 和 r ,保证 l < r (这样就将时间复杂度控制在了 O(N^2^) 内),令
sum = nums[i] + nums[l] + nums[r]如果发现
sum < 0,可以让 l 指针向右移动,使 sum 变大如果发现
sum > 0,可以让 r 指针向左移动,使 sum 变小如果
sum == 0,将值加入到结果中去
由于题目中要求不可以包含重复的三元组,因此在遍历 i、l、r 三个指针时,要注意跳过重复元素
代码如下:
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
int n = nums.length;
Arrays.sort(nums);
// 先确定 i 指针
for (int i = 0; i < n; i ++) {
// i 指针跳过重复元素
if (i > 0 && nums[i] == nums[i-1]) continue;
// 定义 l、r 指针
int l = i + 1, r = n - 1;
while (l < r) {
// 计算三数之和
int sum = nums[i] + nums[l] + nums[r];
// 如果小于 0,l 指针右移,令 sum 变大
if (sum < 0) {
l ++;
continue;
}
// 如果大于 0,r 指针右移,令 sum 变小
if (sum > 0) {
r --;
continue;
}
// 加入结果
res.add(Arrays.asList(nums[i], nums[l], nums[r]));
// l、r 指针跳过重复元素
do l ++; while(l < r && nums[l] == nums[l-1]);
do r --; while(l < r && nums[r] == nums[r+1]);
}
}
return res;
}
}
# LC 25. K 个一组翻转链表(困难)
题目描述:
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
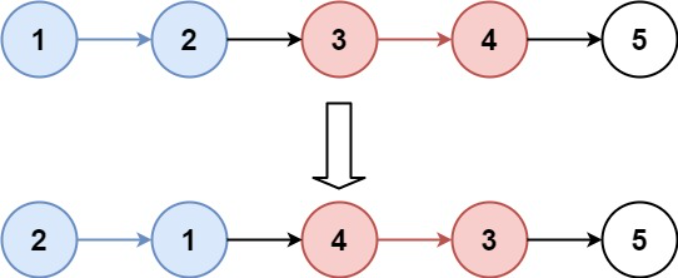
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
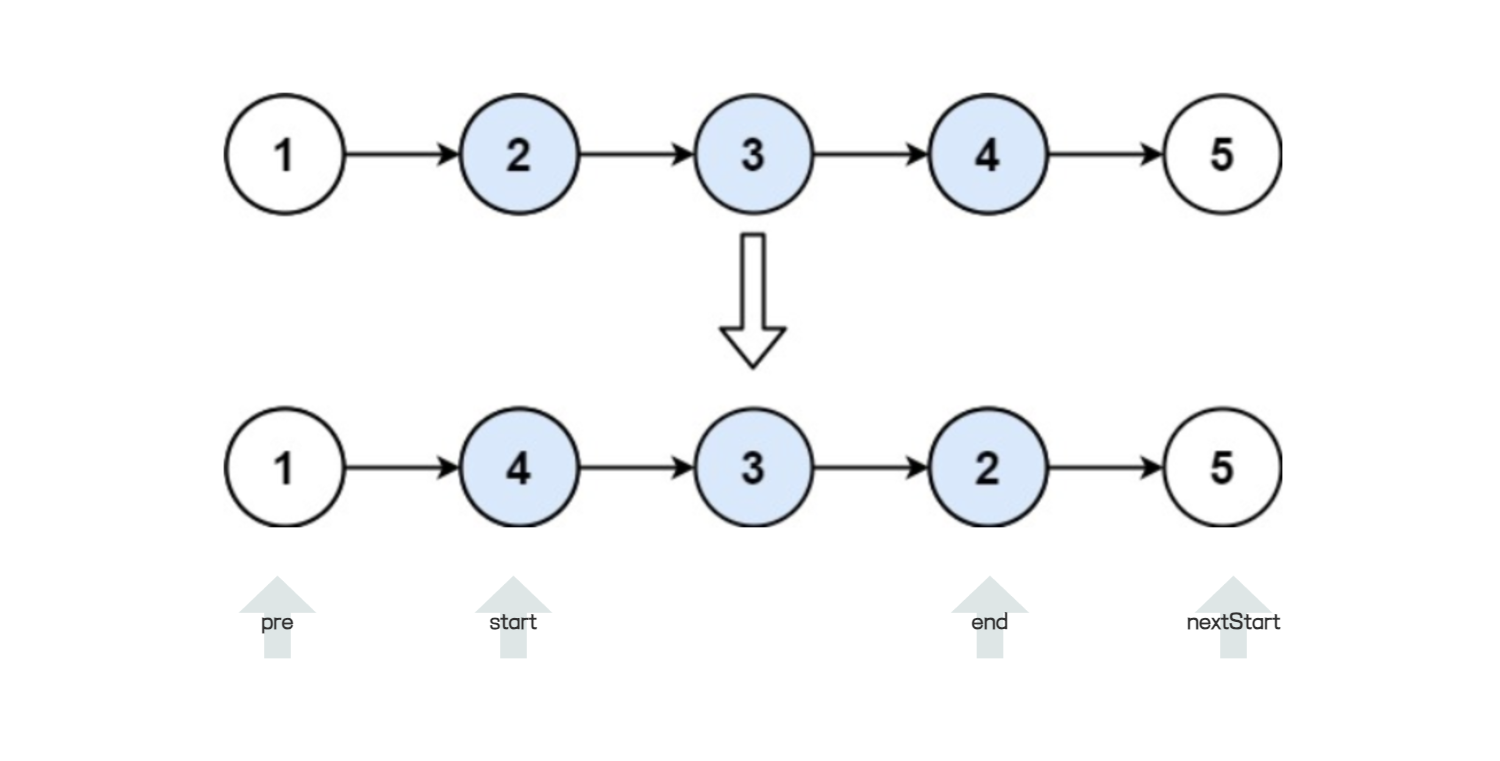
这道题目其实跟之前的反转链表是差不多的,只不过这里要反转多个区间的链表,因此这道题目 比较难的就是定义边界来控制指针的反转
题目说了每隔 k 个节点反转一次,那么我们可以定义一个虚拟头节点 dummy ,再定义三个指针:
- pre 上一个区间的最后一个节点
- start 当前区间的第一个节点
- end 当前区间的最后一个节点
- nextStart 下一个区间的第一个节点
只要有 start 和 end 指针,就可以对这个区间内的链表进行反转,反转之后,还要和前后两个区间连接起来 ,因此需要执行以下代码,来连接三个区间:
pre.next = end;
start.next = nextStart;
四个指针的位置如下图:
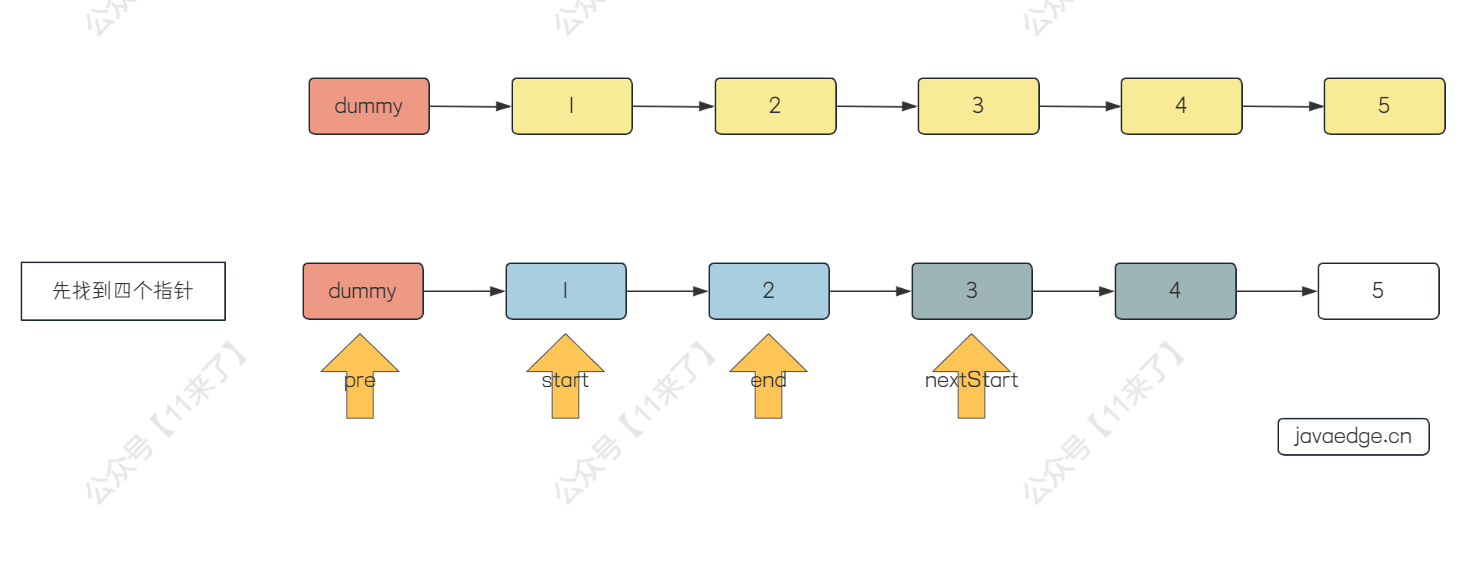
那么只要对 start 和 end 之间的节点反转之后,再和前后两个区间连接,就可以解决了,代码如下:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode dummy = new ListNode(-1);
dummy.next = head;
// 记录上一个区间的最后一个节点
ListNode pre = dummy;
// 记录当前区间的最后一个节点
ListNode end = dummy;
while (true) {
// 找到当前区间的结束节点
for (int i = 0; i < k && end != null; i++)
end = end.next;
if (end == null)
break;
// 记录当前区间的开始节点
ListNode start = pre.next;
// 记录下一个区间的开始节点
ListNode nextStart = end.next;
// 将当前区间的结束节点的 next 设置为空,方便在反转当前区间时控制 while 结束条件
end.next = null;
// 对 start 和 end 之间的节点进行反转
reverse(start);
// 和前边区间连接
pre.next = end;
// 和后边区间连接
start.next = nextStart;
// 更新 pre、end 指针位置
pre = start;
end = pre;
}
return dummy.next;
}
// 进行 start 链表反转(可以多写几遍背下)
public void reverse(ListNode start) {
ListNode now = start;
ListNode last = null;
while (now != null) {
ListNode next = now.next;
now.next = last;
last = now;
now = next;
}
}
}
# LC 200. 岛屿数量(中等)
题目描述:
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
这道题目可以使用 DFS 或者 BFS 来做,其实比较简单,只需要 for 循环遍历所有的网格,如果发现是 1,就对该网格进行 DFS ,将所有相邻并且为 1 的网格置为 0 ,表示是同一片岛屿
那么要遍历相邻的网格,需要使用到一个技巧,我们可以先定义两个数组,表示 x 坐标 和 y 坐标 移动的距离,如下:
// x + dx[0],y + dy[0] 向下走(横坐标不变,纵坐标+1)
// x + dx[1],y + dy[1] 向右走(横坐标+1,纵坐标不动)
// x + dx[2],y + dy[2] 向上走(横坐标不懂,纵坐标-1)
// x + dx[3],y + dy[3] 向左走(横坐标-1,纵坐标不懂)
int[] dx = new int[]{0, 1, 0, -1};
int[] dy = new int[]{1, 0, -1, 0};
再通过一个 for 循环,从当前格子向相邻格子进行移动:
// x、y 为当前各自的坐标
for (int i = 0; i < 4; i ++) {
// 向相邻格子走
int nx = x + dx[i], ny = y + dy[i];
// n 和 m 为地图的长度和宽度,这里是避免走出地图的范围
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
}
代码如下:
class Solution {
int[] dx = new int[]{0, 1, 0, -1};
int[] dy = new int[]{1, 0, -1, 0};
public int numIslands(char[][] g) {
int n = g.length, m = g[0].length;
int res = 0;
for (int i = 0; i < n; i ++) {
for (int j = 0; j < m; j ++) {
// 如果该各自是 1,就对该格子遍历,并记录结果到 res
if (g[i][j] == '1') {
dfs(g, i, j);
res ++;
}
}
}
return res;
}
// 对 x、y 处的岛屿全部置为 0
public void dfs(char[][] g, int x, int y) {
// 记录地图长和宽
int n = g.length, m = g[0].length;
// 将格子置为 0
g[x][y] = '0';
// 向相邻格子进行行走
for (int i = 0; i < 4; i ++) {
int nx = x + dx[i], ny = y + dy[i];
// 避免走出地图,或者走到水里
if (nx < 0 || nx >= n || ny < 0 || ny >= m || g[nx][ny] != '1') continue;
// 对相邻格子继续 dfs
dfs (g, nx, ny);
}
}
}
# LC 31. 下一个排列(中等)
题目描述:
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。 - 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。 - 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
输入:nums = [1,2,3]
输出:[1,3,2]
这道题目是让找出当前排列的下一个排列,也就是 全排列问题
那么我们首先就要了解 全排列 的特性,全排列的 下一个排列 指的是比当前排列更大的一个排列,如果不存在更大的排列的话,就重新组成最小的排列
那么我们要找到下一个排列,就需要将后边的大数和前边的小数来交换,流程如下:
1、将后边尽可能小的【大数】与的前边的小数进行交换
2、将【大数】换到前边之后,需要将【大数】之后的数置为升序
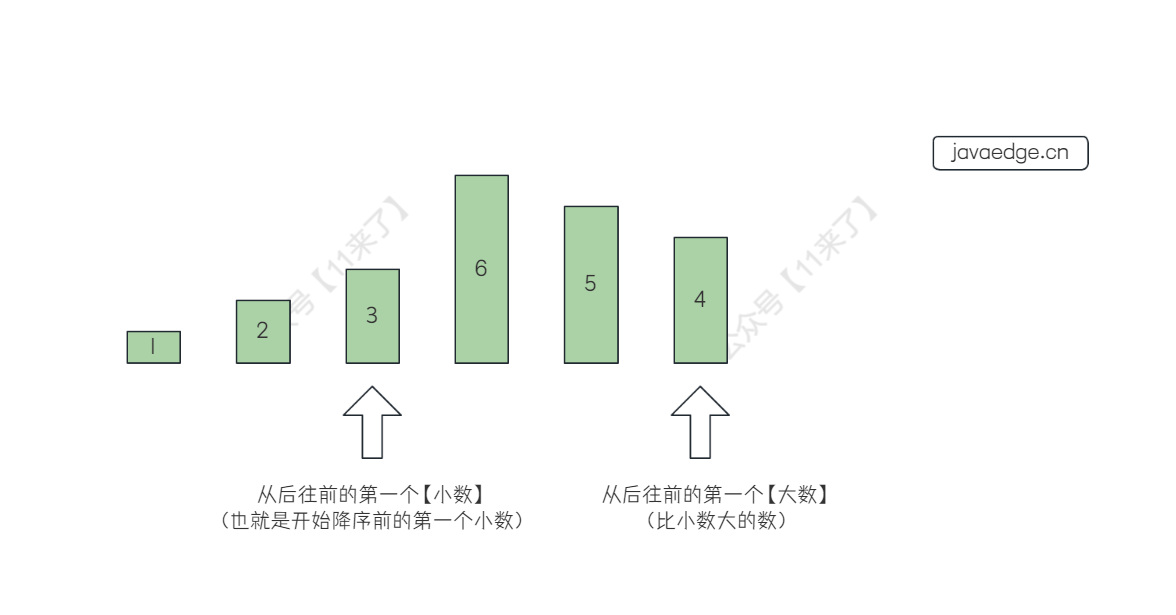
我们可以举一个例子,这样就更加清楚了,比如 123654 的下一个排列是 124356 ,那么先找到 从后往前 的第一个【小数】,也就是 3 ,然后再 从后往前 找到一个最小的【大数】,也就是 4 ,先将 4 和 3 进行交换,交换之后为 124653 ,再将【大数】也就是 4 后边的数置为升序,得到 124356 ,这样就得到了下一个全排列了!
大数、小数如下图:
代码如下:
class Solution {
public void nextPermutation(int[] nums) {
int n = nums.length;
int j = -1;
// 从后边往前,找到第一个【小数】(这个小数是倒序开始位置的前一个数)
for (int i = n-2; i >= 0; i --) {
if (nums[i] < nums[i+1]) {
j = i;
break;
}
}
if (j == -1) {
// 如果没有找到小数,也就是整个排列都是倒序,即 654321,就将排列反转为最小的排列即可
reverse(nums, 0, n - 1);
} else {
// 从后往前找第一个【大数】
for (int i = n - 1; i >= 0; i --) {
// 找到后,就将【大数】和【小数】交换
if (nums[i] > nums[j]) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
break;
}
}
// 将【大数】位置之后的数组置为升序,也就是反转一下
reverse(nums, j + 1, n - 1);
}
}
// 对数组进行反转的 dfs 代码(基础算法)
public void reverse(int[] nums, int l, int r) {
if (l >= r) return;
int tmp = nums[l];
nums[l] = nums[r];
nums[r] = tmp;
reverse(nums, l + 1, r - 1);
}
}
扩展:这里再扩展一下如何实现全排列:通过 DFS + 回溯即可实现
全排列代码如下:
class Solution {
// 记录结果
List<List<Integer>> res = new ArrayList<>();
// 记录每个数是否已经被加入到当前排列中
boolean[] st;
// 记录当前排列
List<Integer> path = new ArrayList<>();
// 数组长度
int n;
public List<List<Integer>> permute(int[] nums) {
n = nums.length;
// 初始化标记数组 st 为 false
st = new boolean[n];
// 开始 dfs 计算全排列
dfs(nums, 0);
return res;
}
// idx 表示计算到全排列中的第几个数
public void dfs(int[] nums, int idx) {
// 如果已经计算了 n 个数了,就将当前排列加入到结果 res 中
if (idx == n) {
// 这里记得创建一个新的 ArrayList 将 path 值赋给新的 List
// 否则,加入到 res 的所有排列都是 path 的引用
res.add(new ArrayList<>(path));
return;
}
// 遍历数组,看哪一个数还可以加入到排列中
for (int i = 0; i < n; i ++) {
// 如果标记为 false,说明当前数可以加入到排列中
if (!st[i]) {
// 标记为 true
st[i] = true;
// 加入到当前排列
path.add(nums[i]);
// 递归下一位的数
dfs(nums, idx + 1);
// 回溯,将当前数从排列中移除
path.remove(path.size() - 1);
// 标记为 false
st[i] = false;
}
}
}
}
# 进阶篇
在进阶篇主要考察 多次二分查找 、 反转链表(区间反转) 、 树形 DP(较为复杂) ,如下:

# LC 852. 山脉数组的峰顶索引(中等)
题目描述:
符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3- 存在
i(0 < i < arr.length - 1)使得:arr[0] < arr[1] < ... arr[i-1] < arr[i]arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
输入:arr = [0,1,0]
输出:1
这道题目是让找出山顶的坐标,并且要求时间复杂度为 O(Logn) ,那么显然 二分查找 的时间复杂度符合要求,并且题目中的数组也符合二分查找的 二段性 ,即分为了 左边升序 的数组和 右边降序 的数组
那么如果发现我们当前二分的 mid 点是在 左边升序数组 中,就令 l = mid ,如果发现 mid 点在右边降序数组中,就令 r = mid - 1
最后 r 指针就是山顶的下标
class Solution {
public int peakIndexInMountainArray(int[] arr) {
int n = arr.length;
// 令 l 为第二个点,r 为 n-2 个点
// 这样 l-1 就不会小于 0 了
int l = 1, r = n - 2;
while (l < r) {
// 如果 r = mid - 1,则 mid = l + r + 1 >> 1
// 如果 r = mid,则 mid = l + r >> 1
int mid = l + r + 1 >> 1;
// 判断在左边升序还是右边降序
if (arr[mid] > arr[mid - 1]) {
l = mid;
} else {
r = mid - 1;
}
}
return r;
}
}
# LC 92. 反转链表 II(中等)
题目描述:
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。

输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
该题目考察的还是 链表的翻转 ,我们只需要对题目中指定的区间内链表翻转即可
那么只要找到 需要翻转的链表区间 ,将该区间链表翻转,再和前边的区间和后边的区间连接起来即可
那么需要翻转指定的链表区间,就需要 2 个指针:
- start :当前翻转区间的开始节点
- end :当前翻转区间的结束节点
翻转之后要和前边、后边的链表区间连接起来,还需要 2 个指针:
- pre :上一个区间的最后一个节点
- nextStart :下一个区间的开始节点
4 个指针位置如下图:
这个和中级篇中的 K 个一组翻转链表的题目类似, 代码如下:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
// 定义一个虚拟节点,方便定位下边 4 个指针的位置
ListNode dummy = new ListNode(-1);
dummy.next = head;
// 上一个区间的最后一个点
ListNode pre = dummy;
// 下一个区间的第一个点
ListNode nextStart = new ListNode(-1);
// 翻转区间的第一个点
ListNode start = new ListNode(-1);
// 翻转区间的最后一个点
ListNode end = new ListNode(-1);
ListNode cur = dummy;
while (cur != null) {
left --;
if (left == 0) {
pre = cur;
start = cur.next;
}
cur = cur.next;
}
cur = dummy;
while (cur != null) {
right --;
cur = cur.next;
if (right == 0) {
end = cur;
nextStart = cur.next;
}
}
end.next = null;
reverse(start);
pre.next = end;
start.next = nextStart;
return dummy.next;
}
public void reverse(ListNode start) {
ListNode last = null;
ListNode now = start;
while (now != null) {
ListNode tmp = now.next;
now.next = last;
last = now;
now = tmp;
}
}
}
# LC 310. 最小高度树(中等)
题目描述:
树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,任何一个没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
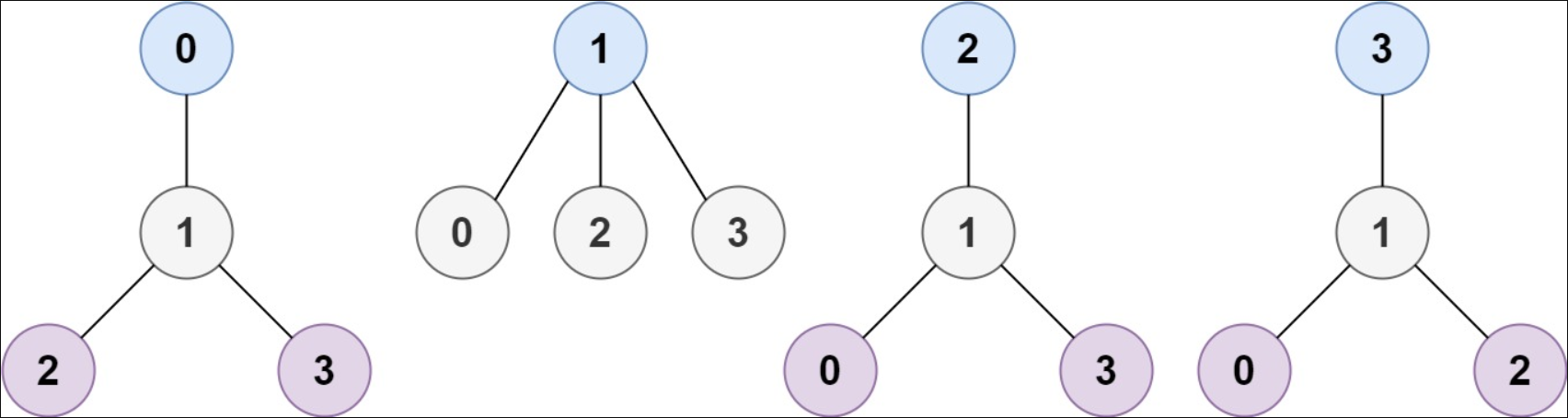
输入:n = 4, edges = [[1,0],[1,2],[1,3]]
输出:[1]
解释:如图所示,当根是标签为 1 的节点时,树的高度是 1 ,这是唯一的最小高度树。
这道题目使用 树形 DP 来做,树形 DP 要么上边的节点使用到了下边节点的状态,要么下边节点使用到了上边节点的状态
这道题目比较复杂,对于一个节点,既使用到了上边、又使用到了下边节点的状态
题目要求我们找到 最小高度 的树,将他们的根节点返回即可,那么如果 暴力 来做的话,只需要去枚举所有的节点,对该节点遍历所有的子树,求出该节点的高度,暴力计算中是会包含许多重复计算的,因此使用 DP 来保存节点的状态,减少计算(暴力解的话,会超时)
要知道一个节点的高度,分为两种情况:
- 该节点向上走的最大高度
- 该节点向下走的最大高度
要计算该节点(设为 x)向上走的最大高度,就是计算该节点的父节点(设为 p)的最大高度 + 1,那么 p 的最大高度也分为了两种情况:
p的最大高度是经过x的:那么这种情况,在计算x的最大高度时,使用到了p的最大高度,而p的最大高度又是走到x了,这样就重复了,所以还需要记录一个数组记录节点的次大高度,这样当p的最大高度是走到x的话,我们直接使用p的次大高度即可p的最大高度不是经过x的:这种情况,就直接使用p的最大高度 + 1 来计算x的最大高度即可

那么在计算的时候,需要使用 d1[i] 来计算 i 节点的最大高度,使用 d2[i] 计算 i 节点的次大高度,使用 up[i] 计算 i 节点向上的最大高度,使用 p[i] 表示 i 节点最大高度是走向的哪个节点(避免重复的计算)
代码如下:
class Solution {
int[] d1;
int[] d2;
int[] p;
int[] up;
Map<Integer, List<Integer>> g = new HashMap<>();
// 计算 u 节点的最大高度和次大高度
public void dfs1(int u, int father) {
List<Integer> toNodes = g.getOrDefault(u, new ArrayList<>());
for (int i = 0; i < toNodes.size(); i ++) {
int x = g.get(u).get(i);
if (x == father) continue;
dfs1(x, u);
int d = d1[x] + 1;
if (d >= d1[u]) {
d2[u] = d1[u];
d1[u] = d;
p[u] = x;
} else if (d > d2[u]) {
d2[u] = d;
}
}
}
// 计算 u 节点向上走的最大高度
void dfs2(int u, int father) {
List<Integer> toNodes = g.getOrDefault(u, new ArrayList<>());
for (int i = 0; i < toNodes.size(); i ++) {
int x = g.get(u).get(i);
if (x == father) continue;
if (p[u] == x) up[x] = Math.max(up[u], d2[u]) + 1;
else up[x] = Math.max(up[u], d1[u]) + 1;
dfs2(x, u);
}
}
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
List<Integer> res = new ArrayList<>();
d1 = new int[n]; d2 = new int[n];
up = new int[n]; p = new int[n];
// 先遍历边,将所有的边放到 g 中去,g[u] 表示 u 节点可以到达节点
for (int i = 0; i < edges.length; i ++) {
int a = edges[i][0];
int b = edges[i][1];
// a 和 b 节点之间存在一条边,是无向边,因此向 g[a]、g[b] 中都存储一份
g.computeIfAbsent(a, k->new ArrayList<>()).add(b);
g.computeIfAbsent(b, k->new ArrayList<>()).add(a);
}
// 计算 u 节点向下走的最大高度和次大高度
dfs1(0, -1);
// 计算 u 节点向上走的最大高度
dfs2(0, -1);
// 先找到最低高度
int minDepth = n + 1;
for (int i = 0; i < n; i ++) {
minDepth = Math.min(minDepth, Math.max(up[i], d1[i]));
}
// 将最低高度的节点加入到结果集中
for (int i = 0; i < n; i ++) {
if (Math.max(up[i], d1[i]) == minDepth) {
res.add(i);
}
}
return res;
}
}
# LC 121. 买卖股票的最佳时机(简单)
题目描述:
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
这道题目在力扣中有一个系列,都是 买卖股票 问题,可以把相关的题目都看一下
这道题目比较简单,遍历一遍,就就可以计算出来最大利润
代码如下:
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
// minv:最低价格
// res:结果
int minv = prices[0], res = 0;
for (int i = 1; i < n; i ++) {
minv = Math.min(minv, prices[i]);
res = Math.max(res, prices[i] - minv);
}
return res;
}
}
