阿里秋招高频算法题汇总！

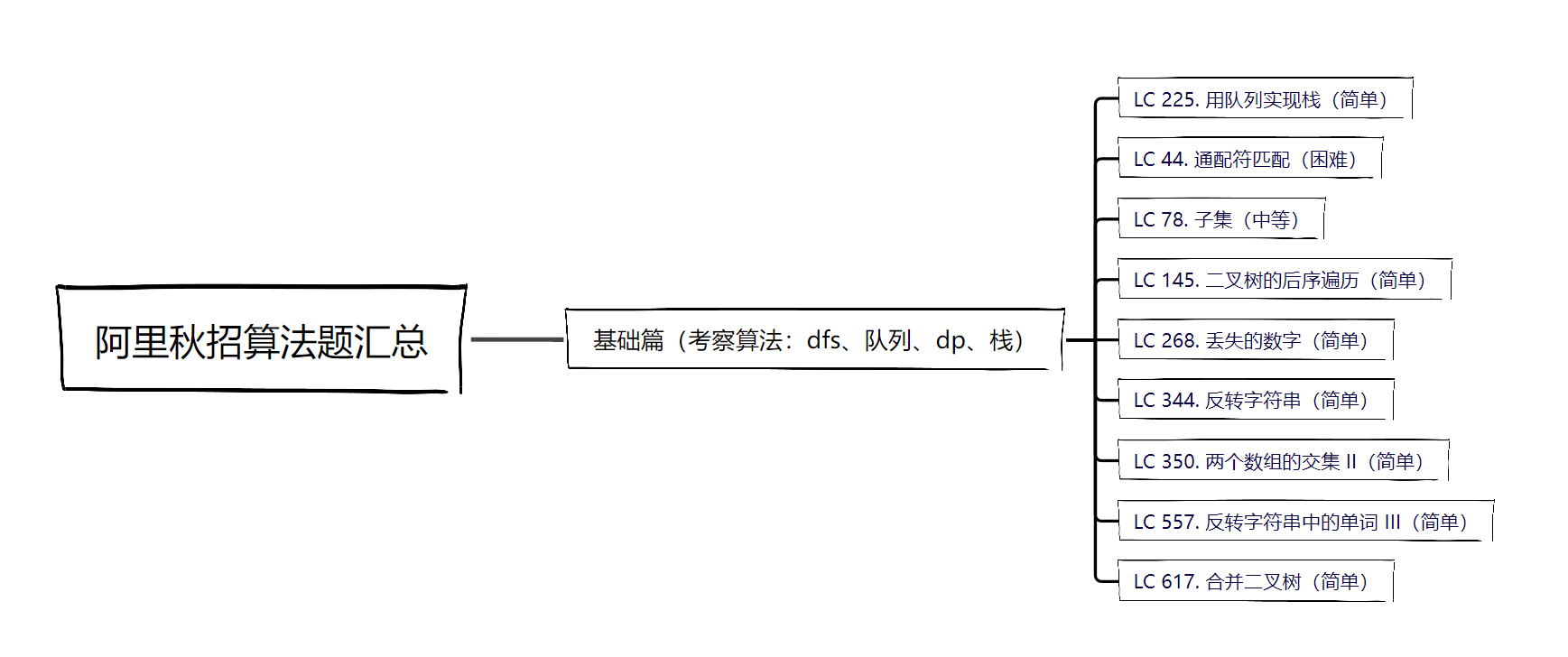
这里讲一下阿里秋招中的高频算法题，分为三个部分： 基础篇 、 中级篇 、 进阶篇

目的就是为了应对秋招中的算法题，其实过算法题的诀窍就在于 理解的基础上 + 背会

看到一个题目，首先要了解题目考察的算法是什么，这个算法要理解，至于具体实现的话，就靠背会了（多写、多练），没有什么捷径！

还有一点要注意的是，在大厂的比试中， 可能考察算法的方式是 ACM 模式 ，这一点和力扣上不同，ACM 模式需要我们自己去引入对应的包，以及自己写算法，力扣是将方法框架给定，只需要在方法内写代码就可以了，这一点要注意！

接下来开始阿里秋招算法的算法讲解，文章内的题目都在 LeetCode 上，因此这里只列出对应的题目序号、题目简介！

基础篇

在基础篇中考察算法更偏向于基础的数据结构，以及 dfs，包括：

• 深度优先搜索：dfs
• 队列
• 动态规划：dp
• 栈

LC 225. 用队列实现栈（简单）

这个考察就是基础数据结构是否会应用 ，题目要求：使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）

实现思路比较简单，队列是 先进先出 ，而栈是 先进后出 ，那么使用队列模拟栈的话，只要使用两个队列，使用【队列1】作为中转，添加的新元素先加入【队列1】，再将【队列2】的元素加入到【队列1】的后边，这样在【队列1】中添加的新元素就在第一个的位置，可以实现栈 最后加入的元素最先被弹出 的特性！

流程如下：

步骤1：先加入元素 A，【队列1】作为中转，因此元素 A 先加入【队列1】

步骤2：再加入元素 B，将 B 先加入【队列1】，此时元素 B 是在第一个位置，再将【队列2】中的元素 A 加入到【队列1】，此时元素顺序就被反转了，符合栈 后入先出 的顺序

可以看到，元素 A 先入队，在队列 2 弹出的时候，元素 A 是最后弹出的，和栈的特性一致，接下来看一下代码实现，注释已经放在代码中了：

class MyStack {
    Queue<Integer> q1;
    Queue<Integer> q2;
    public MyStack() {
        // 初始化两个队列
        q1 = new LinkedList<>();
        q2 = new LinkedList<>();
    }
    // 向栈中加入元素
    public void push(int x) {
        // 先加入到队列 1 中，队列 1 作为一个中转的作用
        q1.offer(x);
        // 将队列 2 的元素一个一个放入队列 1，这样在队列 1 中最后加入的元素其实是在第一个的位置，实现了栈的特性
        while (!q2.isEmpty()) {
            q1.offer(q2.poll());
        }
        // 交换两个队列
        Queue<Integer> tmp = new LinkedList<>();
        tmp = q1;
        q1 = q2;
        q2 = tmp;
    }

    public int pop() {
        // 弹出队列 2 的元素，并返回
        return q2.poll();
    }

    public int top() {
        // 返回队列 2 的队头元素，不弹出
        return q2.peek();
    }

    public boolean empty() {
        // 判空
        return q2.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

LC 44. 通配符匹配（困难）

这个题目是进行字符串匹配，使用 动态规划 DP 来做

动态规划类的问题怎么学？

动态规划类的问题比较吃经验，做的题目如果少的话，看到新的题目一般都是做不出来的，所以对于动态规划类的问题，建议是把我们写过的题型给记住，知道他们的状态是如何转移的，这样就够了，毕竟我们是学习的，并不是发明创造算法的！

题目大致意思就是给定一个字符串 s 和字符模式 p，p 中有通配符 ? 和 * ：

• ? 匹配单个字符
• * 匹配任意字符

答案输出 s 和 p 是否匹配

比如

s = "abc"
p = "a?c"
输出：true 表示 匹配
s = "abc"
p = "*"
输出：true 表示 匹配

首先定义动态规划数组 dp[n][m] ，dp[i][j] 表示 s 的前 i 个字符和 p 的前 j 个字符是否匹配

那么主要分为两种情况：

• 第一种情况：p[j] != * ，如果 p[j] 不是 * 的话

  • 当 p[j] == s[j] 或者 p[j] == ''?' ，此时 s[i] 和 p[j] 是匹配的，那么此时 dp[i][j] 的状态由 dp[i-1][j-1] 转移过来

• 第二种情况：p[j] == * ，这种情况比较复杂，因为我们并不清楚这个 * 到底可以匹配多少个字符，可能匹配 0 个、1个、... j 个字符，如下：

  • 如果匹配 0 个字符，dp[i][j] = dp[i][j-1]
  • 如果匹配 1 个字符，dp[i][j] = dp[i-1][j-1]
  • 如果匹配 2 个字符，dp[i][j] = dp[i-2][j-1]

  那么这样的话，计算 dp 的状态还需要再次遍历一下 i，时间复杂度比较高，因此这里简化一下

  dp[i-1][j] 的状态其实是由 dp[i-1][j-1]、dp[i-2][j-1]... 转移过来，那么这里可以发现 dp[i-1][j] 的状态就符合了上边匹配 1 个、2 个字符的情况，因此这里就不需要进行循环了，此时 dp[i][j] 的状态如下：

  • 如果匹配 0 个字符，dp[i][j] = dp[i][j-1]
  • 如果匹配 1 个、2 个...多个字符，dp[i][j] = dp[i-1][j]

  所以这里 dp 的状态转换简化为： dp[i][j] = dp[i][j-1] && dp[i-1][j]

综上，DP 状态转移主要分为两个状态：

• p[j] != '*' 时，dp[i][j] = dp[i-1][j-1]
• p[j] == '*' 时，dp[i][j] = dp[i][j-1] && dp[i-1][j]

class Solution {
    public boolean isMatch(String s, String p) {
        int n = s.length();
        int m = p.length();
        s = " " + s;
        p = " " + p;
        char[] s1 = s.toCharArray();
        char[] p1 = p.toCharArray();
        boolean[][] dp = new boolean[n+1][m+1];
        // 状态初始化，这个状态影响着后边的状态，所以需要初始化一下
        dp[0][0] = true;

        // i 从 0 开始遍历，因为 dp[0][j] 表示如果 s 串为空串，p 是否匹配 s，这其实是有可能会匹配的，如果 p 全是 * 的话，会匹配
        // 因此 i 从 0 开始遍历，需要对 dp[0][j] 的状态进行设置
        for (int i = 0; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
                if (i > 0 && (s1[i] == p1[j] || p1[j] == '?')) {
                    // 如果字符相等，或者是 ? 通用匹配符的话，dp[i][j] 的状态从 dp[i-1][j-1] 转移而来
                    dp[i][j] = dp[i-1][j-1];
                } else if (p1[j] == '*') {
                    // 这里表示 p[j] 为 * 匹配 0 个字符的情况
                    dp[i][j] = dp[i][j-1];
                    if (i > 0) {
                        // dp[i-1][j] 表示 p[j] 为 * 匹配 1 个、2个...多个字符的情况
                        dp[i][j] = dp[i][j] || dp[i-1][j];
                    }
                }
            }
        }
        return dp[n][m];
    }
}

LC 78. 子集（中等）

这道题是给定一个数组，让你返回所有的子数组，示例输入输出如下：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

可以看到，就是通过不同的排列组合，将所有可能的情况给查出来就好了

这里使用 二进制枚举 来做，对于 nums 数组种的每一位都可能取或者不取，这样就可以枚举出来所有的子数组了，二进制枚举也是比较常用的算法

这里画图举个例子：

可以看到，只需要 枚举所有的二进制 就可以枚举出来所有的子数组了

这里怎么枚举所有的二进制呢？

比如说 nums 数组长度为 3，那么只需要从 0 遍历到 1 <<< 3 - 1 也就是从 0 遍历到 7，这样就可以将所有的二进制全部遍历出来了

代码如下：

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        int n = nums.length;
        // 枚举所有的二进制
        for (int i = 0; i < 1 << n; i++) {
            List<Integer> tmp = new ArrayList<>();
            // 遍历每一位
            for (int j = 0; j < n; j ++) {
                // 如果第 j 位是 1，表示子数组取这一位，加入到子数组 tmp 中去
                if ((i >> j & 1) == 1) {
                    tmp.add(nums[j]);
                }
            }
            res.add(tmp);
        }
        return res;
    }
}

LC 145. 二叉树的后序遍历（简单）

二叉树的遍历其实还是比较容易考察的，这里写两版代码：

• dfs 解决：使用 dfs 解决的话，比较方便
• 迭代解决：迭代解决的话，需要我们手动记录上次访问的节点，来手动实现回溯，因此稍微麻烦一些

后序遍历的话就是先遍历左子树，再遍历右子树，最后遍历根节点，也就是 LRN

dfs 实现

class Solution {
    List<Integer> res = new ArrayList<>();

    public List<Integer> postorderTraversal(TreeNode root) {
        dfs(root);
        return res;
    }

    void dfs(TreeNode root) {
        // 如果到空节点了，就不接着往下走了，返回
        if (root == null) return;
        // 先遍历左子树
        dfs(root.left);
        // 再遍历右子树
        dfs(root.right);
        // 最后是根节点
        res.add(root.val);
    }
}

迭代实现

迭代实现的话，需要我们手动记录上一次节点，来实现回溯

首先要使用栈来记录我们遍历的节点，这里使用链表来模拟栈

之后一直向左子树遍历，当没有左子树之后，就向右子树遍历，在右子树中也还是先向左子树遍历再向右子树遍历

这里定义了 last 节点 来记录回溯的上一个节点，避免回溯之后，由继续向下遍历，导致死循环

这里为了回溯，使用了栈，将元素都推入栈中，当遍历到最底层之后，再从栈中取出元素进行回溯即可！

代码的话，实现的比较精妙（如果有不理解的地方，直接背了就好了，因为这类题型其实是比较固定的），看着流程，自己模拟画图一下就好了， 注意在理解的基础上，可以自己手敲个 3-5 遍，提升一下印象！

class Solution {

    public List<Integer> postorderTraversal(TreeNode root) {
        // 这里使用链表来模拟栈了
        LinkedList<TreeNode> s = new LinkedList<>();
        TreeNode now = root;
        TreeNode last = null;
        List<Integer> res = new ArrayList<>();
        // 如果当前节点为空，并且栈中没有元素了，说明所有元素都遍历完毕了
        while (now != null || !s.isEmpty()) {
            // 如果当前节点不是空，就都压入到栈中
            if (now != null) {
                s.addFirst(now);
                now = now.left;
            } else {
                now = s.getFirst();
                // 如果还有右子树，就往右子树遍历
                // last != now.right 表示可能刚刚才从右子树遍历完回到当前节点，既然回溯了，如果继续向右子树遍历，就反复横跳，死循环了
                if (now.right != null && last != now.right) {
                    now = now.right;
                } else {
                    // 到了这个 if 分支，说明右子树已经为空，或者已经遍历过右子树了
                    // 于是将当前节点加入数组
                    now = s.removeFirst();
                    res.add(now.val);
                    last = now;
                    // 这里将 now 定义为 null，避免重入压入到栈中
                    now = null;
                }
            }
        }
        return res;
    }
}

LC 268. 丢失的数字（简单）

这个题目比较简单了，给定一个数组，长度为 n，找出来 [0, n] 范围内的数字，哪一个数字没有在数组中出现

这里题目给定的数据范围 n 最大为 10^4^ ，所以直接声明一个长度为 n+1 的数组，如果出现过的数字标记为 true，再遍历一遍，标位为 fasle 的表明在数组中没有出现，如下图：

代码如下：

class Solution {
    public int missingNumber(int[] nums) {
        int n = nums.length;
        // 标记数组 0-n
        boolean[] flag = new boolean[n + 1];
        for (int i = 0; i < n; i ++) {
            // 取出 nums[i] 的值，作为下标，在 flag 数组标记
            int idx = nums[i];
            flag[idx] = true;
        }
        for (int i = 0; i <= n; i ++) {
            // 如果标记为 false，说明这个下标没有在 nums 中出现，返回即可
            if (flag[i] == false) {
                return i;
            }
        }
        return -1;
    }
}

LC 344. 反转字符串（简单）

这道题也是简单题，对字符串反转

反转前：hello
反转后：olleh

不过这道题目有一点要求， 只能原地反转 ，不可以定义额外的数组进行操作，因此这里使用 递归 来做

定义一个递归函数 dfs(char[] s, int l, int r) 表示将 s[l] 和 s[r] 进行互换，只要将两边的所有字符串都互换一下就可以了

代码如下：

class Solution {
    public void reverseString(char[] s) {
        int n = s.length;
        // 对 0 和 n-1 位置上的字符互换
        dfs(s, 0, n-1);
    }
    // dfs(s, i, j) 就是将 s[i] 和 s[j] 互换
    public void dfs(char[] s, int l, int r) {
        // 如果左指针 >= 右指针，就不需要反转了，退出递归就好
        if (l >= r) return;

        // 将 left 和 right 位置上的字符串互换进行反转
        char tmp = s[l];
        s[l] = s[r];
        s[r] = tmp;
        dfs(s, l + 1, r - 1);
    }
}

LC 350. 两个数组的交集 II（简单）

这道题目是返回两个数组的交集

给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

如下：

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        Map<Integer, Integer> map = new HashMap<>();
        int n = nums1.length;
        int m = nums2.length;
        for (int i = 0; i < n; i ++) {
            map.put(nums1[i], map.getOrDefault(nums1[i], 0) + 1);
        }
        // 记录交集的数的下标
        int k = 0; 
        for (int i = 0; i < m; i ++) {
            // map 中记录了 nums1 中的所有数字出现的次数
            if (map.containsKey(nums2[i]) && map.get(nums2[i]) > 0) {
                nums1[k ++] = nums2[i];
                // 已经放入到交集数组中了，因此对 nums1 中出现的次数减 1
                map.put(nums2[i], map.get(nums2[i]) - 1);
            }
        }
        // 交集放在了 nums1 数组的 [0, k) 的位置上
        return Arrays.copyOfRange(nums1, 0, k);
    }
}

LC 557. 反转字符串中的单词 III（简单）

这道题目就是让反转字符串中的每一个单词：

输入：s = "Let's take LeetCode contest"
输出："s'teL ekat edoCteeL tsetnoc"

像这一种反转类的题目都可以使用 栈 来做，比如 hello ，按顺序压入栈为：hello，再一个个弹出顺序就反过来为：olleh

这里使用链表来模拟栈了，只操作一边就可以了

class Solution {
    public String reverseWords(String s) {
        StringBuilder res = new StringBuilder("");
        // 使用链表模拟栈
        LinkedList<Character> stack = new LinkedList<>();
        int i = 0, n = s.length();
        while (i < n) {
            while (i < n && s.charAt(i) != ' ') {
                stack.addFirst(s.charAt(i));
                i ++;
            }
            while(!stack.isEmpty()) {
                res.append(stack.removeFirst());
            }
            if (i < n) {
                res.append(" ");
            }
            i ++;
        }
        return res.toString();
    }
}

LC 617. 合并二叉树（简单）

给定两个二叉树，对两个二叉树进行合并，重叠的节点合并为两个节点相加的值，否则，合并为不为 null 的节点值，如下：

使用 dfs 来做，两个树一起递归就可以了，分为三种情况：

• 其中一个树为 null，返回不为 null 的节点
• 两个节点都为 null，返回 null
• 两个节点都不为 null，返回节点相加的值

这里前两种情况可以合并，如果有一个节点为 null，返回另一个节点就可以了，代码如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        // 递归，需要做空判断及时返回
        if (root1 == null) return root2;
        if (root2 == null) return root1;
        // 对两个节点合并
        TreeNode mergedNode = new TreeNode(root1.val + root2.val);
        // 对左子树合并
        mergedNode.left = mergeTrees(root1.left, root2.left);
        // 对右子树合并
        mergedNode.right = mergeTrees(root1.right, root2.right);
        return mergedNode;
    }
}

中级篇

在中级篇中主要考察的算法更加偏向于 链表 、 动态规划 这两个方面，包括：

• 双链表的实现以及基于双链表实现 LRU
• 动态规划
• 链表操作

LC 146. LRU 缓存（中等）

题目简述：

请你设计并实现一个满足LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

LRU 缓存淘汰策略还是比较常用的，并且实现起来不算复杂，同时考察了对基础数据结构的掌握，因此在面试或者笔试中出现的概率还是不小的，建议要好好掌握一下

实现的话，我们自己定义一个 Node 数据结构，并定义 prev 指针 和 next 指针 ，来自己实现一个双向链表，常用的元素在链表头部，不常用的在尾部，我们向链表中插入一个 虚拟头节点 dummy 就可以在 O(1) 的时间复杂度内获取到头节点和尾节点

如果新插入元素的话，就放在头节点，如果查询一个元素，就将该元素移动到链表头，表示最近刚使用过，如下：

class LRUCache {
    // 定义节点，实现双向链表
    private static class Node {
        int k, v;
        Node prev,next;
        Node (int k, int v) {
            this.k = k;
            this.v = v;
        }
    }

    // 虚拟头节点
    Node dummy = new Node(-1, -1);
    // 存储 key 对应的 Node 节点
    Map<Integer, Node> nodes = new HashMap<>();
    // LRU 缓存容量
    int capacity;
    // LRU 中元素数量
    int size;

    // 初始化
    public LRUCache(int capacity) {
        this.capacity = capacity;
        this.size = 0;
        dummy.prev = dummy;
        dummy.next = dummy;
    }

    public int get(int key) {
        Node node = nodes.get(key);
        if (node == null) return -1;
        pushToFront(node);
        return node.v;
    }

    // 将 node 节点移动至链表头
    private void pushToFront(Node node) {
        // 将 node 从当前位置删除
        removeNode(node);
        addToFront(node);
    }

    // 将 node 放到链表头
    private void addToFront(Node node) {
        node.prev = dummy;
        node.next = dummy.next;
        dummy.next.prev = node;
        dummy.next = node;
    }

    public void put(int key, int value) {
        Node node = nodes.get(key);
        // 如果节点不为空，更新值，并放入头部
        if (node != null) {
            node.v = value;
            nodes.put(key, node);
            pushToFront(node);
        } else {
            // 如果节点为空，插入新的节点
            size ++;
            // 如果超过 LRU 容量，移除最长最久未使用的节点
            if (size > capacity) {
                Node tail = dummy.prev;
                // 移除最后一个不常使用的节点
                nodes.remove(tail.k);
                removeNode(tail);
                this.size --;
            }
            node = new Node(key, value);
            addToFront(node);
            nodes.put(key, node);
        }
    }

    // 移除指定节点
    private void removeNode(Node node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    // 打印 LRU 中存储的数据情况，方便看出哪些数据被淘汰
    public void printLRUCache() {
        Node node = dummy.next;
        while (node != dummy) {
            System.out.print("k=" + node.k + ":v=" + node.v + " ");
            node = node.next;
        }
        System.out.println();
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

LC 22. 括号生成（中等）

题目描述：

给定一个数字 n ，生成所有有效的括号组合

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

这里就是枚举出来所有有效的括号组合，必须保证 每一个左括号都有一个右括号与之对应

保证括号组合有效的话，我们可以通过剩余未使用的左括号和右括号的数量来快速判断:

• 如果剩余的左括号的数量 大于 右括号的数量，那么说明会存在部分左括号找不到对应的右括号对应，因此肯定不合法

这里解题的话直接使用 dfs 枚举所有的情况，也就是对当前字符串，加左括号和加右括号两种情况都试一下，将不合法的情况给及时回溯掉就可以了

class Solution {
    List<String> res = new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        dfs("", n, n);
        return res;
    }
    // str 表示当前枚举的括号，l 表示剩余可用左括号、r 表示剩余可用右括号
    public void dfs(String str, int l, int r) {
        // 将错误情况排除掉
        if (l < 0 || l > r) return;
        // 如果括号用完了，就加入到结果集
        if (l == 0 && r == 0) {
            res.add(str);
            return;
        }

        // 接下来，要么加左括号，要么加右括号
        dfs(str + "(", l - 1, r);
        dfs (str + ")", l, r - 1);
    }
}

LC 206. 反转链表（简单）

题目描述：

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

这道题目代码不算太难，只是稍微有点绕，而且这一种链表的题目还是比较常见的

这里我们在 原地进行反转链表 ，不额外申请空间（额外申请空间的话，就比较简单了）

那么只需要定义一个 last 、 next 、 now 节点，用来存储当前节点以及上一个和下一个节点，就可以进行翻转了，如下图：

/**
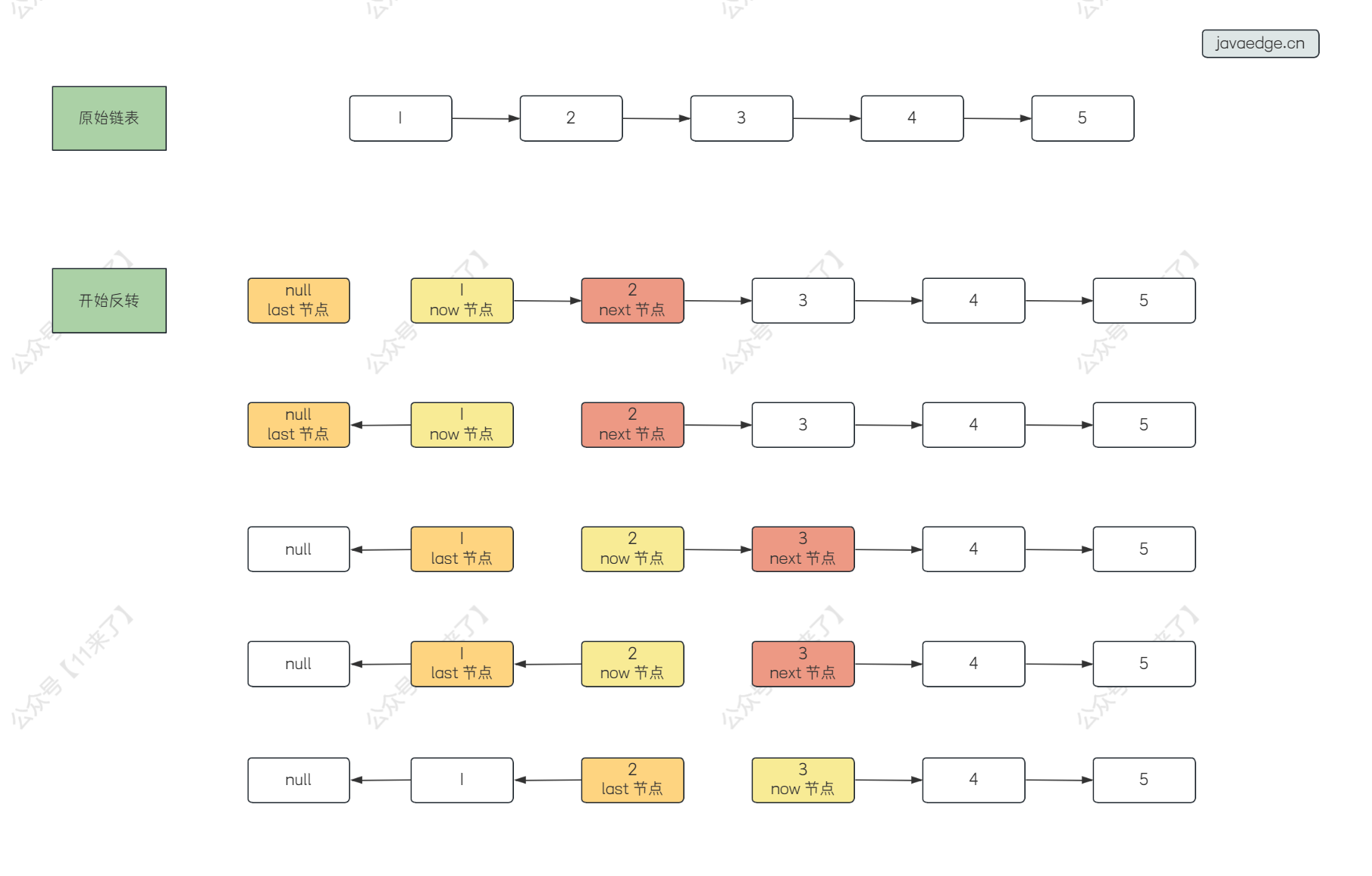
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode last = null;
        ListNode now = head;
        while (now != null) {
            ListNode next = now.next;
            now.next = last;
            last = now;
            now = next;
        }
        return last;
    }
}

LC 21. 合并两个有序链表（简单）

题目描述：

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

解题思路比较简单，同时遍历两个链表，挑一个数值比较小的加入到结果链表中就可以了！

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        // 定义结果链表的头节点
        ListNode head = new ListNode(-1);
        ListNode now = head;
        while (true) {
            // 找到数值较小的节点，加入到结果链表
            if (l1 != null && l2 != null) {
                if (l1.val < l2.val) {
                    now.next = new ListNode(l1.val);
                    now = now.next;
                    l1 = l1.next;
                }  else {
                    now.next = new ListNode(l2.val);
                    now = now.next;
                    l2 = l2.next;
                }
            } else if (l1 == null) {
                // 如果 l1 链表后边没元素了，就将 l2 链表后边的元素拼到结果链表后
                now.next = l2;
                break;
            } else if (l2 == null) {
                // 如果 l2 链表后边没元素了，就将 l1 链表后边的元素拼到结果链表后
                now.next = l1;
                break;
            }
        }
        // 返回头节点后的数据
        return head.next;
    }
}

进阶篇

在进阶篇中主要考察的算法更加偏向于 动态规划 、 DFS 、 双指针 这几个方面，这些都是高频考点：

• 动态规划（高频考点）
• DFS（高频考点）
• 双指针（高频考点）

LC 237. 删除链表中的节点（中等）

题目描述：

现在有一个单链表，给定一个 node 节点，让你删除这个 node 节点

输入：head = [4,5,1,9], node = 5
输出：[4,1,9]
解释：指定链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9

题目给定 node 节点，并没有给定这个单链表的 head 节点，因此你是无法找到 node 节点的前置节点，所以肯定 无法删除 node 节点

解题思路就是将 node 节点的下一个节点值赋给当前 node 节点，将 node 的下一个节点删除掉

（这道题感觉有点像脑筋急转弯）

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public void deleteNode(ListNode node) {
        node.val = node.next.val;
        node.next = node.next.next;
    }
}

LC 152. 乘积最大子数组（中等）

题目描述：

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

首先要找到乘积最大的子数组，那么这个最大成绩可能是 任何个区间内 的子数组的乘积

先说一下 暴力解法 ，只需要出来所有的子区间，再去计算乘积就好了，这个暴力解法的时间复杂度是 O(N^3^) ，比较高，所以考虑 优化 一下

使用 动态规划 来进行优化：

• f[i] 表示在数组 0-i 中，选取 nums[i] 时的最大乘积
• g[i] 表示在数组 0-i 中，选取 nums[i] 时的最小乘积

题目中给出的数都是整数，没有小数，所以乘积的绝对值只要不碰到 0 就会越来越大，那么我们可以使用 f[i] 记录从 0 到 i 的最大的乘积，使用 g[i] 记录从 0 到 i 的最小的乘积，那么遍历数组，就有两种情况：

• 如果当前 nums[i] 不是 0，于是取 $f[i] = max(nums[i] * f[i-1], nums[i] * g[i-1])$ ，取 $g[i] = min(nums[i] * f[i-1], nums[i] * g[i-1])$ ，这样就可以维护 f 和 g 数组的值了
• 如果当前 nums[i] 是 0，那么 nums[i] 和任意数乘积都为 0，那么就是当前区间就被隔断了，接着从下一个区间开始计算就好（如果不理解，可以手动计算一下就好）

计算流程如下：

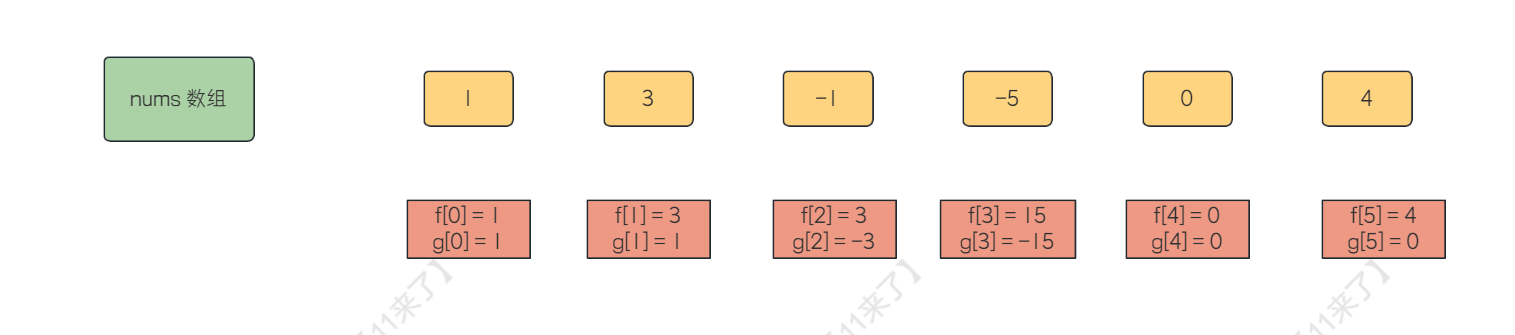
可以发现， f[i] 的状态只与 f[i-1] 有关，因此还可以进行空间优化，这里就不需要维护一个数组了，直接使用 f 变量来进行状态转移就好了

class Solution {
    public int maxProduct(int[] nums) {
        int n = nums.length;
        int f = 1;
        int g = 1;
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < n; i ++) {
            // 计算和最大乘积相乘的结果
            int fi = nums[i] * f;
            // 计算和最小乘积相乘的结果
            int gi = nums[i] * g;
            // 如果 nums[i-1] 是 0 的话，那么 fi 一定是 0，这里计算最大乘积的话，就不能和 fi 相乘了
            // 因此如果 fi 和 gi 是 0 的话，那么这里还要和 nums[i] 判断一下取最大值
            f = Math.max(nums[i], Math.max(fi, gi));
            g = Math.min(nums[i], Math.min(fi, gi));
            // 每一次子区间都计算一下最大值
            res = Math.max(f, res);
        }
        return res;
    }
}

LC 279. 完全平方数（中等）

题目描述：

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

这道题目使用 动态规划 来解，对于给定的 n 来说，并不知道它是由几个完全平方数组成的，所以如果暴力计算的话，时间复杂度是比较高的，使用 动态规划 进行状态转移来优化

定义动态规划数组 f[i] ：

• f[i] 表示组成 i 的完全平方数的最少个数

对于 i 来说，最差情况下就是由 i 个 1 组成，所以可以初始化 f[i] = i

状态转移 的话，对于 i 来枚举 j ，转移方程为：$f[i] = min(f[i], f[i-j*j] + 1)$

也就是 f[i] 的状态可以由 f[i- j*j] 转移而来，j*j 也是一个完全平方数，因此 $f[i] = f[i-j*j] + 1$

class Solution {
    public int numSquares(int n) {
        int[] f = new int[n+1];
        for (int i = 1; i <= n; i ++) {
            f[i] = i;
            // 枚举 j 的话，注意控制条件 i-j*j >= 0，避免数组越界
            for (int j = 1; i - j * j >= 0; j ++) {
                // 状态转移
                f[i] = Math.min(f[i], f[i- j*j] + 1);
            }
        }
        return f[n];
    }
}

LC 93. 复原 IP 地址（中等）

题目描述：

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

• 例如："0.1.2.201" 和"192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

这道题目中，限制了 s 字符串的长度最大为 20，所以可以直接 dfs 暴力接触所有情况就可以

ip 地址由 4 个整数组成，我们就去枚举每一个数，当枚举完 4 个数之后，并且遍历完了整个 s 字符串，说明这次的 ip 是合法的，加入到结果集中

这里枚举数的时候，还要注意不能有前导 0，并且不能超过 255

代码如下：

class Solution {
    List<String> res = new ArrayList<>();
    public List<String> restoreIpAddresses(String s) {
        dfs(0, 0, s, "");
        return res;
    }
    // u：已经枚举的整数的个数
    // k：枚举到 s 中的下标
    // cur：当前已经组好的 ip 地址
    public void dfs(int u, int k, String s, String cur) {
        // 如果枚举完 4 个数
        if (u == 4) {
            // 并且已经遍历完 s 字符串
            if (k == s.length()) {
                // 这里将 cur 的最后一个 . 给截取掉
                res.add(cur.substring(0, cur.length() - 1));
            }
            // 定义递归终点
            return;
        }

        // 计算当前这一个整数的值
        int sum = 0;
        // 从下标 k 开始枚举当前这一个整数的值
        for (int i = k; i < s.length(); i ++) {
            // 如果第 k 位是 0，由于不能有前导 0，因此 0 后边不可以跟其他数了，直接 break 掉就好
            if (i > k && s.charAt(k) == '0') break;
            // 上一位作为十分位了，因此乘上 10，计算这一个整数的和
            sum = sum * 10 + s.charAt(i) - '0';
            // 如果 sum <= 255 的话，这一位是合法的，递归继续搜
            if (sum <= 255) dfs(u + 1, i + 1, s, cur + String.valueOf(sum) + ".");
            // 如果 sum 超过 255 的话，已经不合法了，没必要递归搜索了
            else break;
        }
    }
}

LC 3. 无重复字符的最长子串（中等）

题目描述：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

这道题考察了 双指针 ，定义两个指针 l 和 r ，判断 l ~ r 这一段区间内有无重复字符，记录最长字串长度即可

使用哈希表 cnt 对每个字符的出现次数计数

两个指针的 移动规则 如下：

• l 指针 ：如果发现 l ~ r 区间内有重复字符，就将 l 指针右移，直到没有重复字符
• r 指针 ：每次右移一个位置，将当前字符在 cnt 数组中计数

代码如下：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int l = 0, r = 0;
        int res = 0;
        int n = s.length();
        Map<Character, Integer> cnt = new HashMap<>();
        while (r < n) {
            char ch = s.charAt(r);
            // 如果发现 l-r 区间内有重复的字符
            while (cnt.containsKey(ch)) {
                // 删除左指针对应的字符
                cnt.remove(s.charAt(l));
                // 左指针右移
                l ++;
            }
            // 将当前字符加入 cnt 中记录
            cnt.put(ch, 1);
            // 记录最大区间长度
            res = Math.max(res, r - l + 1); 
            // 右移右指针
            r ++;
        }
        return res;
    }
}

LC 409. 最长回文串（简单）

题目描述：

给定一个包含大写字母和小写字母的字符串 s ，返回 通过这些字母构造成的 最长的回文串 。

在构造过程中，请注意 区分大小写 。比如 "Aa" 不能当做一个回文字符串。

输入:s = "abccccdd"
输出:7
解释:
我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。

这一道题的话，就是给一个字符串，你可以选择任意字符来构成回文串，看构造的最长回文串的长度

这道题也没有考某一个算法，主要是 回文串的特性 ：

• 回文串长度为偶数 ：只要有两个相同的字符，那么一个放左边，一个放右边，肯定是可以构成回文串的
• 回文串长度为奇数 ：这种情况的话，中间还可以放一个字符，不需要对应的字符，如 aba ，b 可以放在中间，构成奇数长度的回文串

解题思路 就是遍历字符串 s ，一个字符出现的次数为偶数，就一定可以组成回文串，直接将偶数次数的字符加到回文长度即可

再判断字符串 s 中是否有出现奇数次的字符，如果有的话，可以将奇数的字符放在中间，回文串的长度还可以加 1

代码如下：

class Solution {
    public int longestPalindrome(String s) {
        // 结果
        int res = 0;
        // 记录每个字符出现的次数，char 是 1 个字节，最多只有 128 个 char，因此这里数组长度声明为 128
        char[] ch = new char[128];
        for(int i = 0; i < s.length(); i++){
            char c = s.charAt(i);
            ch[c]++;
            if (ch[c] == 2){
                res += 2;
                ch[c] = 0;
            }
        }
        if(s.length() % ) res += 1;
        return res;
    }
}

LC 88. 合并两个有序数组（简单）

题目描述：

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

**注意：**最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

这道题目也是 双指针 ，同时遍历两个数组，取较小的值就好了，实现起来比较简单，就不细说了

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int sum = m + n;
        int[] res = new int[sum];
        int idx = 0;
        int i = 0, j = 0;
        // 遍历两个数组，当两个数组都没有遍历结束
        while(i < m && j < n){
            int a = nums1[i];
            int b = nums2[j];
            // 取较小值，放入到结果数组
            if (a < b){
                res[idx ++] = a;
                i ++;
            }else{
                res[idx ++] = b;
                j ++;
            }
        }
        // 两个数组长度可能不同，一个数组遍历完，另一个可能还没有，这里对没有遍历完的数组继续遍历
        while(i < m){
            res[idx ++] = nums1[i ++];
        }
        while(j < n){
            res[idx ++] = nums2[j ++];
        }
        nums1 = res;
        // 结果要求需要放在 nums1 数组中，这里赋值一下
        for (int cc = 0; cc < idx; cc ++) {
            nums1[cc] = res[cc];
        }
    }
}

LC 1143. 最长公共子序列（中等）

题目描述：

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

这道题目要求出两个字符串的 最长公共子序列 ，如果暴力做的话，需要枚举每一个字符串的子序列，再对子序列判断是否相同，这样时间复杂度直接 爆表 了，面试官肯定也不愿意看到这样的写法！

还是 动态规划 来做，先说动态规划数组 含义 ：

• f[i][j] ：表示第一字符串的前 i 个字符和第二个字符串的前 j 个字符的最长公共子序列

假设两个字符串为 s1 和 s2 ，那么 状态转移 为：

• 如果 $s1[i] == s2[j]$ ，那么 $f[i][j] = f[i-1][j-1] + 1$ ，也就是 f[i][j] 的状态由 f[i-1][j-1] 转移而来，并且 s1[i] == s2[j] ，因此这里长度再加一
• 如果 $s1[i] != s2[j]$ ，那么分为两种情况：
  • 忽略 s1[i] ，那么 f[i][j] 状态由 f[i-1][j] 转移过来
  • 忽略 s2[j] ，那么 f[i][j] 状态由 f[i][j-1] 转移过来

代码如下 ：

class Solution {
    public int longestCommonSubsequence(String s1, String s2) {
        int n = s1.length(), m = s2.length();
        // dp 题一般下标从 1 开始计算，这样 i-1 就不会小于 0 了
        int[][] f = new int[n+1][m+1];
        s1 = " " + s1;
        s2 = " " + s2;
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
                // 分为两种情况进行状态转移
                if (s1.charAt(i) == s2.charAt(j)) {
                    f[i][j] = f[i-1][j-1] + 1;
                } else {
                    f[i][j] = Math.max(f[i-1][j], f[i][j-1]);
                }
            }
        }
        return f[n][m];
    }
}