 07.ConcurrentHashMap源码分析
07.ConcurrentHashMap源码分析
转载自:@Author 马士兵教育-郑金维
# ConcurrentHashMap
# 一、存储结构
ConcurrentHashMap是线程安全的HashMap
ConcurrentHashMap在JDK1.8中是以CAS+synchronized实现的线程安全
CAS:在没有hash冲突时(Node要放在数组上时)
synchronized:在出现hash冲突时(Node存放的位置已经有数据了)
存储的结构:数组+链表+红黑树

# 二、存储操作
# 2.1 put方法
public V put(K key, V value) {
// 在调用put方法时,会调用putVal,第三个参数默认传递为false
// 在调用putIfAbsent时,会调用putVal方法,第三个参数传递的为true
// 如果传递为false,代表key一致时,直接覆盖数据
// 如果传递为true,代表key一致时,什么都不做,key不存在,正常添加(Redis,setnx)
return putVal(key, value, false);
}
# 2.2 putVal方法-散列算法
final V putVal(K key, V value, boolean onlyIfAbsent) {
// ConcurrentHashMap不允许key或者value出现为null的值,跟HashMap的区别
if (key == null || value == null) throw new NullPointerException();
// 根据key的hashCode计算出一个hash值,后期得出当前key-value要存储在哪个数组索引位置
int hash = spread(key.hashCode());
// 一个标识,在后面有用!
int binCount = 0;
// 省略大量的代码……
}
// 计算当前Node的hash值的方法
static final int spread(int h) {
// 将key的hashCode值的高低16位进行^运算,最终又与HASH_BITS进行了&运算
// 将高位的hash也参与到计算索引位置的运算当中
// 为什么HashMap、ConcurrentHashMap,都要求数组长度为2^n
// HASH_BITS让hash值的最高位符号位肯定为0,代表当前hash值默认情况下一定是正数,因为hash值为负数时,有特殊的含义
// static final int MOVED = -1; // 代表当前hash位置的数据正在扩容!
// static final int TREEBIN = -2; // 代表当前hash位置下挂载的是一个红黑树
// static final int RESERVED = -3; // 预留当前索引位置……
return (h ^ (h >>> 16)) & HASH_BITS;
// 计算数组放到哪个索引位置的方法 (f = tabAt(tab, i = (n - 1) & hash)
// n:是数组的长度
}
00001101 00001101 00101111 10001111 - h = key.hashCode
运算方式
00000000 00000000 00000000 00001111 - 15 (n - 1)
&
(
(
00001101 00001101 00101111 10001111 - h
^
00000000 00000000 00001101 00001101 - h >>> 16
)
&
01111111 11111111 11111111 11111111 - HASH_BITS
)
# 2.3 putVal方法-添加数据到数组&初始化数组
final V putVal(K key, V value, boolean onlyIfAbsent) {
// 省略部分代码…………
// 将Map的数组赋值给tab,死循环
for (Node<K,V>[] tab = table;;) {
// 声明了一堆变量~~
// n:数组长度
// i:当前Node需要存放的索引位置
// f: 当前数组i索引位置的Node对象
// fn:当前数组i索引位置上数据的hash值
Node<K,V> f; int n, i, fh;
// 判断当前数组是否还没有初始化
if (tab == null || (n = tab.length) == 0)
// 将数组进行初始化。
tab = initTable();
// 基于 (n - 1) & hash 计算出当前Node需要存放在哪个索引位置
// 基于tabAt获取到i位置的数据
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
// 现在数组的i位置上没有数据,基于CAS的方式将数据存在i位置上
if (casTabAt(tab, i, null,new Node<K,V>(hash, key, value, null)))
// 如果成功,执行break跳出循环,插入数据成功
break;
}
// 判断当前位置数据是否正在扩容……
else if ((fh = f.hash) == MOVED)
// 让当前插入数据的线程协助扩容
tab = helpTransfer(tab, f);
// 省略部分代码…………
}
// 省略部分代码…………
}
sizeCtl:是数组在初始化和扩容操作时的一个控制变量
-1:代表当前数组正在初始化
小于-1:低16位代表当前数组正在扩容的线程个数(如果1个线程扩容,值为-2,如果2个线程扩容,值为-3)
0:代表数据还没初始化
大于0:代表当前数组的扩容阈值,或者是当前数组的初始化大小
// 初始化数组方法
private final Node<K,V>[] initTable() {
// 声明标识
Node<K,V>[] tab; int sc;
// 再次判断数组没有初始化,并且完成tab的赋值
while ((tab = table) == null || tab.length == 0) {
// 将sizeCtl赋值给sc变量,并判断是否小于0
if ((sc = sizeCtl) < 0)
Thread.yield();
// 可以尝试初始化数组,线程会以CAS的方式,将sizeCtl修改为-1,代表当前线程可以初始化数组
else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
// 尝试初始化!
try {
// 再次判断当前数组是否已经初始化完毕。
if ((tab = table) == null || tab.length == 0) {
// 开始初始化,
// 如果sizeCtl > 0,就初始化sizeCtl长度的数组
// 如果sizeCtl == 0,就初始化默认的长度
int n = (sc > 0) ? sc : DEFAULT_CAPACITY;
// 初始化数组!
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
// 将初始化的数组nt,赋值给tab和table
table = tab = nt;
// sc赋值为了数组长度 - 数组长度 右移 2位 16 - 4 = 12
// 将sc赋值为下次扩容的阈值
sc = n - (n >>> 2);
}
} finally {
// 将赋值好的sc,设置给sizeCtl
sizeCtl = sc;
}
break;
}
}
return tab;
}
# 2.4 putVal方法-添加数据到链表
final V putVal(K key, V value, boolean onlyIfAbsent) {
// 省略部分代码…………
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
// n:数组长度
// i:当前Node需要存放的索引位置
// f: 当前数组i索引位置的Node对象
// fn:当前数组i索引位置上数据的hash值
// 省略部分代码…………
else {
// 声明变量为oldVal
V oldVal = null;
// 基于当前索引位置的Node,作为锁对象……
synchronized (f) {
// 判断当前位置的数据还是之前的f么……(避免并发操作的安全问题)
if (tabAt(tab, i) == f) {
// 再次判断hash值是否大于0(不是树)
if (fh >= 0) {
// binCount设置为1(在链表情况下,记录链表长度的一个标识)
binCount = 1;
// 死循环,每循环一次,对binCount
for (Node<K,V> e = f;; ++binCount) {
// 声明标识ek
K ek;
// 当前i索引位置的数据,是否和当前put的key的hash值一致
if (e.hash == hash &&
// 如果当前i索引位置数据的key和put的key == 返回为true
// 或者equals相等
((ek = e.key) == key || (ek != null && key.equals(ek)))) {
// key一致,可能需要覆盖数据!
// 当前i索引位置数据的value复制给oldVal
oldVal = e.val;
// 如果传入的是false,代表key一致,覆盖value
// 如果传入的是true,代表key一致,什么都不做!
if (!onlyIfAbsent)
// 覆盖value
e.val = value;
break;
}
// 拿到当前指定的Node对象
Node<K,V> pred = e;
// 将e指向下一个Node对象,如果next指向的是一个null,可以挂在当前Node下面
if ((e = e.next) == null) {
// 将hash,key,value封装为Node对象,挂在pred的next上
pred.next = new Node<K,V>(hash, key,
value, null);
break;
}
}
}
// 省略部分代码…………
}
}
// binCount长度不为0
if (binCount != 0) {
// binCount是否大于8(链表长度是否 >= 8)
if (binCount >= TREEIFY_THRESHOLD)
// 尝试转为红黑树或者扩容
// 基于treeifyBin方法和上面的if判断,可以得知链表想要转为红黑树,必须保证数组长度大于等于64,并且链表长度大于等于8
// 如果数组长度没有达到64的话,会首先将数组扩容
treeifyBin(tab, i);
// 如果出现了数据覆盖的情况,
if (oldVal != null)
// 返回之前的值
return oldVal;
break;
}
}
}
// 省略部分代码…………
}
// 为什么链表长度为8转换为红黑树,不是能其他数值嘛?
// 因为布松分布
The main disadvantage of per-bin locks is that other update
* operations on other nodes in a bin list protected by the same
* lock can stall, for example when user equals() or mapping
* functions take a long time. However, statistically, under
* random hash codes, this is not a common problem. Ideally, the
* frequency of nodes in bins follows a Poisson distribution
* (http://en.wikipedia.org/wiki/Poisson_distribution) with a
* parameter of about 0.5 on average, given the resizing threshold
* of 0.75, although with a large variance because of resizing
* granularity. Ignoring variance, the expected occurrences of
* list size k are (exp(-0.5) * pow(0.5, k) / factorial(k)). The
* first values are:
*
* 0: 0.60653066
* 1: 0.30326533
* 2: 0.07581633
* 3: 0.01263606
* 4: 0.00157952
* 5: 0.00015795
* 6: 0.00001316
* 7: 0.00000094
* 8: 0.00000006
* more: less than 1 in ten million
# 三、扩容操作
# 3.1 treeifyBin方法触发扩容
// 在链表长度大于等于8时,尝试将链表转为红黑树
private final void treeifyBin(Node<K,V>[] tab, int index) {
Node<K,V> b; int n, sc;
// 数组不能为空
if (tab != null) {
// 数组的长度n,是否小于64
if ((n = tab.length) < MIN_TREEIFY_CAPACITY)
// 如果数组长度小于64,不能将链表转为红黑树,先尝试扩容操作
tryPresize(n << 1);
// 省略部分代码……
}
}
# 3.2 tryPreSize方法-针对putAll的初始化操作
// size是将之前的数组长度 左移 1位得到的结果
private final void tryPresize(int size) {
// 如果扩容的长度达到了最大值,就使用最大值
// 否则需要保证数组的长度为2的n次幂
// 这块的操作,是为了初始化操作准备的,因为调用putAll方法时,也会触发tryPresize方法
// 如果刚刚new的ConcurrentHashMap直接调用了putAll方法的话,会通过tryPresize方法进行初始化
int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY :
tableSizeFor(size + (size >>> 1) + 1);
// 这些代码和initTable一模一样
// 声明sc
int sc;
// 将sizeCtl的值赋值给sc,并判断是否大于0,这里代表没有初始化操作,也没有扩容操作
while ((sc = sizeCtl) >= 0) {
// 将ConcurrentHashMap的table赋值给tab,并声明数组长度n
Node<K,V>[] tab = table; int n;
// 数组是否需要初始化
if (tab == null || (n = tab.length) == 0) {
// 进来执行初始化
// sc是初始化长度,初始化长度如果比计算出来的c要大的话,直接使用sc,如果没有sc大,
// 说明sc无法容纳下putAll中传入的map,使用更大的数组长度
n = (sc > c) ? sc : c;
// 设置sizeCtl为-1,代表初始化操作
if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
try {
// 再次判断数组的引用有没有变化
if (table == tab) {
// 初始化数组
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
// 数组赋值
table = nt;
// 计算扩容阈值
sc = n - (n >>> 2);
}
} finally {
// 最终赋值给sizeCtl
sizeCtl = sc;
}
}
}
// 如果计算出来的长度c如果小于等于sc,直接退出循环结束方法
// 数组长度大于等于最大长度了,直接退出循环结束方法
else if (c <= sc || n >= MAXIMUM_CAPACITY)
break;
// 省略部分代码
}
}
// 将c这个长度设置到最近的2的n次幂的值, 15 - 16 17 - 32
// c == size + (size >>> 1) + 1
// size = 17
00000000 00000000 00000000 00010001
+
00000000 00000000 00000000 00001000
+
00000000 00000000 00000000 00000001
// c = 26
00000000 00000000 00000000 00011010
private static final int tableSizeFor(int c) {
// 00000000 00000000 00000000 00011001
int n = c - 1;
// 00000000 00000000 00000000 00011001
// 00000000 00000000 00000000 00001100
// 00000000 00000000 00000000 00011101
n |= n >>> 1;
// 00000000 00000000 00000000 00011101
// 00000000 00000000 00000000 00000111
// 00000000 00000000 00000000 00011111
n |= n >>> 2;
// 00000000 00000000 00000000 00011111
// 00000000 00000000 00000000 00000001
// 00000000 00000000 00000000 00011111
n |= n >>> 4;
// 00000000 00000000 00000000 00011111
// 00000000 00000000 00000000 00000000
// 00000000 00000000 00000000 00011111
n |= n >>> 8;
// 00000000 00000000 00000000 00011111
n |= n >>> 16;
// 00000000 00000000 00000000 00100000
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
# 3.3 tryPreSize方法-计算扩容戳并且查看BUG
private final void tryPresize(int size) {
// n:数组长度
while ((sc = sizeCtl) >= 0) {
// 判断当前的tab是否和table一致,
else if (tab == table) {
// 计算扩容表示戳,根据当前数组的长度计算一个16位的扩容戳
// 第一个作用是为了保证后面的sizeCtl赋值时,保证sizeCtl为小于-1的负数
// 第二个作用用来记录当前是从什么长度开始扩容的
int rs = resizeStamp(n);
// BUG --- sc < 0,永远进不去~
// 如果sc小于0,代表有线程正在扩容。
if (sc < 0) {
// 省略部分代码……协助扩容的代码(进不来~~~~)
}
// 代表没有线程正在扩容,我是第一个扩容的。
else if (U.compareAndSwapInt(this, SIZECTL, sc,
(rs << RESIZE_STAMP_SHIFT) + 2))
// 省略部分代码……第一个扩容的线程……
}
}
}
// 计算扩容表示戳
// 32 = 00000000 00000000 00000000 00100000
// Integer.numberOfLeadingZeros(32) = 26
// 1 << (RESIZE_STAMP_BITS - 1)
// 00000000 00000000 10000000 00000000
// 00000000 00000000 00000000 00011010
// 00000000 00000000 10000000 00011010
static final int resizeStamp(int n) {
return Integer.numberOfLeadingZeros(n) | (1 << (RESIZE_STAMP_BITS - 1));
}
# 3.4 tryPreSize方法-对sizeCtl的修改以及条件判断的BUG
private final void tryPresize(int size) {
// sc默认为sizeCtl
while ((sc = sizeCtl) >= 0) {
else if (tab == table) {
// rs:扩容戳 00000000 00000000 10000000 00011010
int rs = resizeStamp(n);
if (sc < 0) {
// 说明有线程正在扩容,过来帮助扩容
Node<K,V>[] nt;
// 依然有BUG
// 当前线程扩容时,老数组长度是否和我当前线程扩容时的老数组长度一致
// 00000000 00000000 10000000 00011010
if ((sc >>> RESIZE_STAMP_SHIFT) != rs
// 10000000 00011010 00000000 00000010
// 00000000 00000000 10000000 00011010
// 这两个判断都是有问题的,核心问题就应该先将rs左移16位,再追加当前值。
// 这两个判断是BUG
// 判断当前扩容是否已经即将结束
|| sc == rs + 1 // sc == rs << 16 + 1 BUG
// 判断当前扩容的线程是否达到了最大限度
|| sc == rs + MAX_RESIZERS // sc == rs << 16 + MAX_RESIZERS BUG
// 扩容已经结束了。
|| (nt = nextTable) == null
// 记录迁移的索引位置,从高位往低位迁移,也代表扩容即将结束。
|| transferIndex <= 0)
break;
// 如果线程需要协助扩容,首先就是对sizeCtl进行+1操作,代表当前要进来一个线程协助扩容
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
// 上面的判断没进去的话,nt就代表新数组
transfer(tab, nt);
}
// 是第一个来扩容的线程
// 基于CAS将sizeCtl修改为 10000000 00011010 00000000 00000010
// 将扩容戳左移16位之后,符号位是1,就代码这个值为负数
// 低16位在表示当前正在扩容的线程有多少个,
// 为什么低位值为2时,代表有一个线程正在扩容
// 每一个线程扩容完毕后,会对低16位进行-1操作,当最后一个线程扩容完毕后,减1的结果还是-1,
// 当值为-1时,要对老数组进行一波扫描,查看是否有遗漏的数据没有迁移到新数组
else if (U.compareAndSwapInt(this, SIZECTL, sc,(rs << RESIZE_STAMP_SHIFT) + 2))
// 调用transfer方法,并且将第二个参数设置为null,就代表是第一次来扩容!
transfer(tab, null);
}
}
}
# 3.5 transfer方法-计算每个线程迁移的长度
// 开始扩容 tab=oldTable
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
// n = 数组长度
// stride = 每个线程一次性迁移多少数据到新数组
int n = tab.length, stride;
// 基于CPU的内核数量来计算,每个线程一次性迁移多少长度的数据最合理
// NCPU = 4
// 举个栗子:数组长度为1024 - 512 - 256 - 128 / 4 = 32
// MIN_TRANSFER_STRIDE = 16,为每个线程迁移数据的最小长度
if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE)
stride = MIN_TRANSFER_STRIDE;
// 根据CPU计算每个线程一次迁移多长的数据到新数组,如果结果大于16,使用计算结果。 如果结果小于16,就使用最小长度16
}
# 3.6 transfer方法-构建新数组并查看标识属性
// 以32长度数组扩容到64位例子
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
// n = 老数组长度 32
// stride = 步长 16
// 第一个进来扩容的线程需要把新数组构建出来
if (nextTab == null) {
try {
// 将原数组长度左移一位,构建新数组长度
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1];
// 赋值操作
nextTab = nt;
} catch (Throwable ex) {
// 到这说明已经达到数组长度的最大取值范围
sizeCtl = Integer.MAX_VALUE;
// 设置sizeCtl后直接结束
return;
}
// 将成员变量的新数组赋值
nextTable = nextTab;
// 迁移数据时,用到的标识,默认值为老数组长度
transferIndex = n; // 32
}
// 新数组长度
int nextn = nextTab.length; // 64
// 在老数组迁移完数据后,做的标识
ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab);
// 迁移数据时,需要用到的标识
boolean advance = true;
boolean finishing = false;
// 省略部分代码
}
# 3.7 transfer方法-线程领取迁移任务

// 以32长度扩容到64位为例子
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
// n:32
// stride:16
int n = tab.length, stride;
if (nextTab == null) {
// 省略部分代码…………
// nextTable:新数组
nextTable = nextTab;
// transferIndex:0
transferIndex = n;
}
// nextn:64
int nextn = nextTab.length;
ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab);
// advance:true,代表当前线程需要接收任务,然后再执行迁移, 如果为false,代表已经接收完任务
boolean advance = true;
// finishing:false,是否迁移结束!
boolean finishing = false;
// 循环……
// i = 15 代表当前线程迁移数据的索引值!!
// bound = 0
for (int i = 0, bound = 0;;) {
// f = null
// fh = 0
Node<K,V> f; int fh;
// 当前线程要接收任务
while (advance) {
// nextIndex = 16
// nextBound = 16
int nextIndex, nextBound;
// 第一次进来,这两个判断肯定进不去。
// 对i进行--,并且判断当前任务是否处理完毕!
if (--i >= bound || finishing)
advance = false;
// 判断transferIndex是否小于等于0,代表没有任务可领取,结束了。
// 在线程领取任务会,会对transferIndex进行修改,修改为transferIndex - stride
// 在任务都领取完之后,transferIndex肯定是小于等于0的,代表没有迁移数据的任务可以领取
else if ((nextIndex = transferIndex) <= 0) {
i = -1;
advance = false;
}
// 当前线程尝试领取任务
else if (U.compareAndSwapInt
(this, TRANSFERINDEX, nextIndex,
nextBound = (nextIndex > stride ? nextIndex - stride : 0))) {
// 对bound赋值
bound = nextBound;
// 对i赋值
i = nextIndex - 1;
// 设置advance设置为false,代表当前线程领取到任务了。
advance = false;
}
}
// 开始迁移数据,并且在迁移完毕后,会将advance设置为true
}
}
# 3.8 transfer方法-迁移结束操作
// 以32长度扩容到64位为例子
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
for (int i = 0, bound = 0;;) {
while (advance) {
// 判断扩容是否已经结束!
// i < 0:当前线程没有接收到任务!
// i >= n: 迁移的索引位置,不可能大于数组的长度,不会成立
// i + n >= nextn:因为i最大值就是数组索引的最大值,不会成立
if (i < 0 || i >= n || i + n >= nextn) {
// 如果进来,代表当前线程没有接收到任务
int sc;
// finishing为true,代表扩容结束
if (finishing) {
// 将nextTable新数组设置为null
nextTable = null;
// 将当前数组的引用指向了新数组~
table = nextTab;
// 重新计算扩容阈值 64 - 16 = 48
sizeCtl = (n << 1) - (n >>> 1);
// 结束扩容
return;
}
// 当前线程没有接收到任务,让当前线程结束扩容操作。
// 采用CAS的方式,将sizeCtl - 1,代表当前并发扩容的线程数 - 1
if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) {
// sizeCtl的高16位是基于数组长度计算的扩容戳,低16位是当前正在扩容的线程个数
if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT)
// 代表当前线程并不是最后一个退出扩容的线程,直接结束当前线程扩容
return;
// 如果是最后一个退出扩容的线程,将finishing和advance设置为true
finishing = advance = true;
// 将i设置为老数组长度,让最后一个线程再从尾到头再次检查一下,是否数据全部迁移完毕。
i = n;
}
}
// 开始迁移数据,并且在迁移完毕后,会将advance设置为true
}
}
# 3.9 transfer方法-迁移数据(链表)
// 以32长度扩容到64位为例子
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
// 省略部分代码…………
for (int i = 0, bound = 0;;) {
// 省略部分代码…………
if (i < 0 || i >= n || i + n >= nextn) {
// 省略部分代码…………
}
// 开始迁移数据,并且在迁移完毕后,会将advance设置为true
// 获取指定i位置的Node对象,并且判断是否为null
else if ((f = tabAt(tab, i)) == null)
// 当前桶位置没有数据,无需迁移,直接将当前桶位置设置为fwd
advance = casTabAt(tab, i, null, fwd);
// 拿到当前i位置的hash值,如果为MOVED,证明数据已经迁移过了。
else if ((fh = f.hash) == MOVED)
// 一般是给最后扫描时,使用的判断,如果迁移完毕,直接跳过当前位置。
advance = true; // already processed
else {
// 当前桶位置有数据,先锁住当前桶位置。
synchronized (f) {
// 判断之前取出的数据是否为当前的数据。
if (tabAt(tab, i) == f) {
// ln:null - lowNode
// hn:null - highNode
Node<K,V> ln, hn;
// hash大于0,代表当前Node属于正常情况,不是红黑树,使用链表方式迁移数据
if (fh >= 0) {
// lastRun机制
// 000000000010000
// 这种运算结果只有两种,要么是0,要么是n
int runBit = fh & n;
// 将f赋值给lastRun
Node<K,V> lastRun = f;
// 循环的目的就是为了得到链表下经过hash & n结算,结果一致的最后一些数据
// 在迁移数据时,值需要迁移到lastRun即可,剩下的指针不需要变换。
for (Node<K,V> p = f.next; p != null; p = p.next) {
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
// runBit == 0,赋值给ln
if (runBit == 0) {
ln = lastRun;
hn = null;
}
// rubBit == n,赋值给hn
else {
hn = lastRun;
ln = null;
}
// 循环到lastRun指向的数据即可,后续不需要再遍历
for (Node<K,V> p = f; p != lastRun; p = p.next) {
// 获取当前Node的hash值,key值,value值。
int ph = p.hash; K pk = p.key; V pv = p.val;
// 如果hash&n为0,挂到lowNode上
if ((ph & n) == 0)
ln = new Node<K,V>(ph, pk, pv, ln);
// 如果hash&n为n,挂到highNode上
else
hn = new Node<K,V>(ph, pk, pv, hn);
}
// 采用CAS的方式,将ln挂到新数组的原位置
setTabAt(nextTab, i, ln);
// 采用CAS的方式,将hn挂到新数组的原位置 + 老数组长度
setTabAt(nextTab, i + n, hn);
// 采用CAS的方式,将当前桶位置设置为fwd
setTabAt(tab, i, fwd);
// advance设置为true,保证可以进入到while循环,对i进行--操作
advance = true;
}
// 省略迁移红黑树的操作
}
}
}
}
}
# 3.10 helpTransfer方法-协助扩容
// 在添加数据时,如果插入节点的位置的数据,hash值为-1,代表当前索引位置数据已经被迁移到了新数组
// tab:老数组
// f:数组上的Node节点
final Node<K,V>[] helpTransfer(Node<K,V>[] tab, Node<K,V> f) {
// nextTab:新数组
// sc:给sizeCtl做临时变量
Node<K,V>[] nextTab; int sc;
// 第一个判断:老数组不为null
// 第二个判断:新数组不为null (将新数组赋值给nextTab)
if (tab != null &&
(f instanceof ForwardingNode) && (nextTab = ((ForwardingNode<K,V>)f).nextTable) != null) {
// ConcurrentHashMap正在扩容
// 基于老数组长度计算扩容戳
int rs = resizeStamp(tab.length);
// 第一个判断:fwd中的新数组,和当前正在扩容的新数组是否相等。 相等:可以协助扩容。不相等:要么扩容结束,要么开启了新的扩容
// 第二个判断:老数组是否改变了。 相等:可以协助扩容。不相等:扩容结束了
// 第三个判断:如果正在扩容,sizeCtl肯定为负数,并且给sc赋值
while (nextTab == nextTable && table == tab && (sc = sizeCtl) < 0) {
// 第一个判断:将sc右移16位,判断是否与扩容戳一致。 如果不一致,说明扩容长度不一样,退出协助扩容
// 第二个、三个判断是BUG:
/*
sc == rs << 16 + 1 || 如果+1和当前sc一致,说明扩容已经到了最后检查的阶段
sc == rs << 16 + MAX_RESIZERS || 判断协助扩容的线程是否已经达到了最大值
*/
// 第四个判断:transferIndex是从高索引位置到低索引位置领取数据的一个核心属性,如果满足 小于等于0,说明任务被领光了。
if ((sc >>> RESIZE_STAMP_SHIFT) != rs ||
sc == rs + 1 ||
sc == rs + MAX_RESIZERS ||
transferIndex <= 0)
// 不需要协助扩容
break;
// 将sizeCtl + 1,进来协助扩容
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) {
// 协助扩容
transfer(tab, nextTab);
break;
}
}
return nextTab;
}
return table;
}
# 四、红黑树操作
在前面搞定了关于数据+链表的添加和扩容操作,现在要搞定红黑树。因为红黑树的操作有点乱,先对红黑树结构有一定了解。
# 4.1 什么是红黑树
红黑树是一种特殊的平衡二叉树,首选具备了平衡二叉树的特点:左子树和右子数的高度差不会超过1,如果超过了,平衡二叉树就会基于左旋和右旋的操作,实现自平衡。
红黑树在保证自平衡的前提下,还保证了自己的几个特性:
- 每个节点必须是红色或者黑色。
- 根节点必须是黑色。
- 如果当前节点是红色,子节点必须是黑色
- 所有叶子节点都是黑色。
- 从任意节点到每个叶子节点的路径中,黑色节点的数量是相同的。
当对红黑树进行增删操作时,可能会破坏平衡或者是特性,这是红黑树就需要基于左旋、右旋、变色来保证平衡和特性。
左旋操作:
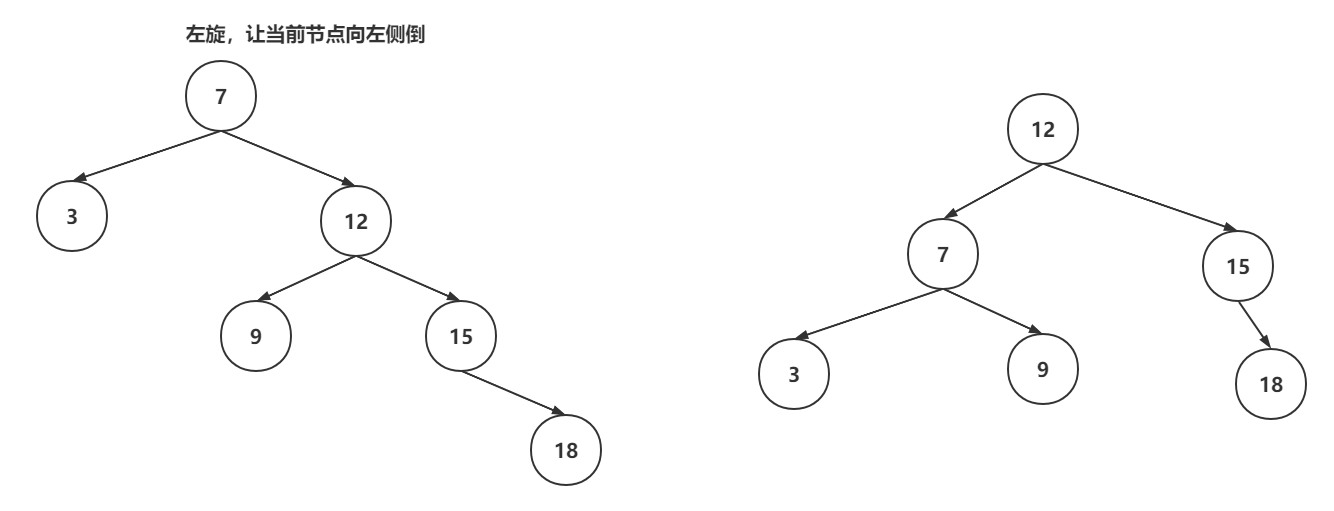
右旋操作:
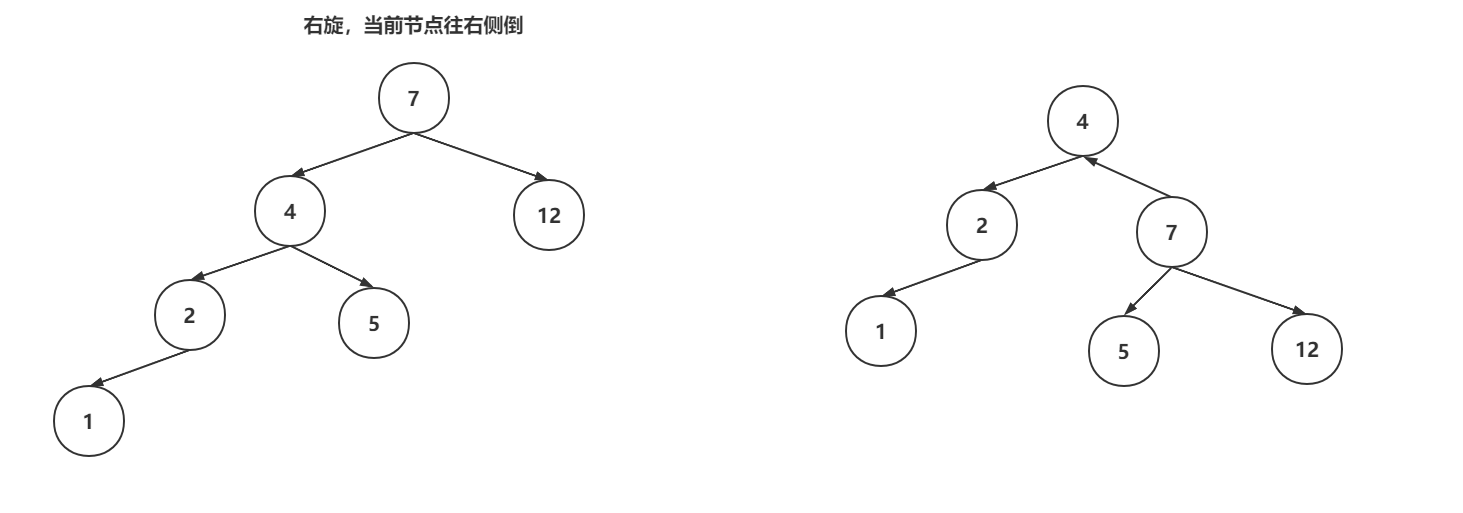
变色操作:节点的颜色从黑色变为红色,或者从红色变为黑色,就成为变色。变色操作是在增删数据之后,可能出现的操作。插入数据时,插入节点的颜色一般是红色,因为插入红色节点的破坏红黑树结构的可能性比较低的。如果破坏了红黑树特性,会通过变色来调整
红黑树相对比较复杂,完整的红黑树代码400~500行内容,没有必要全部记下来,或者首先红黑树。
如果向细粒度掌握红黑树的结构:https://www.mashibing.com/subject/21?courseNo=339
# 4.2 TreeifyBin方法-封装TreeNode和双向链表
// 将链表转为红黑树的准备操作
private final void treeifyBin(Node<K,V>[] tab, int index) {
// b:当前索引位置的Node
Node<K,V> b; int sc;
if (tab != null) {
// 省略部分代码
// 开启链表转红黑树操作
// 当前桶内有数据,并且是链表结构
else if ((b = tabAt(tab, index)) != null && b.hash >= 0) {
// 加锁,保证线程安全
synchronized (b) {
// 再次判断数据是否有变化,DCL
if (tabAt(tab, index) == b) {
// 开启准备操作,将之前的链表中的每一个Node,封装为TreeNode,作为双向链表
// hd:是整个双向链表的第一个节点。
// tl:是单向链表转换双向链表的临时存储变量
TreeNode<K,V> hd = null, tl = null;
for (Node<K,V> e = b; e != null; e = e.next) {
TreeNode<K,V> p = new TreeNode<K,V>(e.hash, e.key, e.val, null, null);
if ((p.prev = tl) == null)
hd = p;
else
tl.next = p;
tl = p;
}
// hd就是整个双向链表
// TreeBin的有参构建,将双向链表转为了红黑树。
setTabAt(tab, index, new TreeBin<K,V>(hd));
}
}
}
}
}
# 4.3 TreeBin有参构造-双向链表转为红黑树
TreeBin中不但保存了红黑树结构,同时还保存在一套双向链表
// 将双向链表转为红黑树的操作。 b:双向链表的第一个节点
// TreeBin继承自Node,root:代表树的根节点,first:双向链表的头节点
TreeBin(TreeNode<K,V> b) {
// 构建Node,并且将hash值设置为-2
super(TREEBIN, null, null, null);
// 将双向链表的头节点赋值给first
this.first = b;
// 声明r的TreeNode,最后会被赋值为根节点
TreeNode<K,V> r = null;
// 遍历之前封装好的双向链表
for (TreeNode<K,V> x = b, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
// 先将左右子节点清空
x.left = x.right = null;
// 如果根节点为null,第一次循环
if (r == null) {
// 将第一个节点设置为当前红黑树的根节点
x.parent = null; // 根节点没父节点
x.red = false; // 不是红色,是黑色
r = x; // 将当前节点设置为r
}
// 已经有根节点,当前插入的节点要作为父节点的左子树或者右子树
else {
// 拿到了当前节点key和hash值。
K k = x.key;
int h = x.hash;
Class<?> kc = null;
// 循环?
for (TreeNode<K,V> p = r;;) {
// dir:如果为-1,代表要插入到父节点的左边,如果为1,代表要插入的父节点的右边
// ph:是父节点的hash值
int dir, ph;
// pk:是父节点的key
K pk = p.key;
// 父节点的hash值,大于当前节点的hash值,就设置为-1,代表要插入到父节点的左边
if ((ph = p.hash) > h)
dir = -1;
// 父节点的hash值,小于当前节点的hash值,就设置为1,代表要插入到父节点的右边
else if (ph < h)
dir = 1;
// 父节点的hash值和当前节点hash值一致,基于compare方式判断到底放在左子树还是右子树
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
// 拿到当前父节点。
TreeNode<K,V> xp = p;
// 将p指向p的left、right,并且判断是否为null
// 如果为null,代表可以插入到这位置。
if ((p = (dir <= 0) ? p.left : p.right) == null) {
// 进来就说明找到要存放当前节点的位置了
// 将当前节点的parent指向父节点
x.parent = xp;
// 根据dir的值,将父节点的left、right指向当前节点
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 插入一个节点后,做一波平衡操作
r = balanceInsertion(r, x);
break;
}
}
}
}
// 将根节点复制给root
this.root = r;
// 检查红黑树结构
assert checkInvariants(root);
}
# 4.4 balanceInsertion方法-保证红黑树平衡以及特性
// 红黑树的插入动画:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
// 红黑树做自平衡以及保证特性的操作。 root:根节点, x:当前节点
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) {
// 先将节点置位红色
x.red = true;
// xp:父节点
// xpp:爷爷节点
// xppl:爷爷节点的左子树
// xxpr:爷爷节点的右子树
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// 拿到父节点,并且父节点为红
if ((xp = x.parent) == null) {
// 当前节点为根节点,置位黑色
x.red = false;
return x;
}
// 父节点不是红色,爷爷节点为null
else if (!xp.red || (xpp = xp.parent) == null)
// 什么都不做,直接返回
return root;
// =====================================
// 左子树的操作
if (xp == (xppl = xpp.left)) {
// 通过变色满足红黑树特性
if ((xppr = xpp.right) != null && xppr.red) {
// 叔叔节点和父节点变为黑色
xppr.red = false;
xp.red = false;
// 爷爷节点置位红色
xpp.red = true;
// 让爷爷节点作为当前节点,再走一次循环
x = xpp;
}
else {
// 如果当前节点是右子树,通过父节点的左旋,变为左子树的结构
if (x == xp.right) {、
// 父节点做左旋操作
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
// 父节点变为黑色
xp.red = false;
if (xpp != null) {
// 爷爷节点变为红色
xpp.red = true;
// 爷爷节点做右旋操作
root = rotateRight(root, xpp);
}
}
}
}
// 右子树(只讲左子树就足够了,因为业务都是一样的)
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
# 4.5 putTreeVal方法-添加节点
整体操作就是判断当前节点要插入到左子树,还是右子数,还是覆盖操作。
确定左子树和右子数之后,直接维护双向链表和红黑树结构,并且再判断是否需要自平衡。
TreeBin的双向链表用的头插法。
// 添加节点到红黑树内部
final TreeNode<K,V> putTreeVal(int h, K k, V v) {
// Class对象
Class<?> kc = null;
// 搜索节点
boolean searched = false;
// 死循环,p节点是根节点的临时引用
for (TreeNode<K,V> p = root;;) {
// dir:确定节点是插入到左子树还是右子数
// ph:父节点的hash值
// pk:父节点的key
int dir, ph; K pk;
// 根节点是否为诶null,把当前节点置位根节点
if (p == null) {
first = root = new TreeNode<K,V>(h, k, v, null, null);
break;
}
// 判断当前节点要放在左子树还是右子数
else if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
// 如果key一致,直接返回p,由putVal去修改数据
else if ((pk = p.key) == k || (pk != null && k.equals(pk)))
return p;
// hash值一致,但是key的==和equals都不一样,基于Compare去判断
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
// 基于compare判断也是一致,就进到if判断
(dir = compareComparables(kc, k, pk)) == 0) {
// 开启搜索,查看是否有相同的key,只有第一次循环会执行。
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.findTreeNode(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.findTreeNode(h, k, kc)) != null))
// 如果找到直接返回
return q;
}
// 再次判断hash大小,如果小于等于,返回-1
dir = tieBreakOrder(k, pk);
}
// xp是父节点的临时引用
TreeNode<K,V> xp = p;
// 基于dir判断是插入左子树还有右子数,并且给p重新赋值
if ((p = (dir <= 0) ? p.left : p.right) == null) {
// first引用拿到
TreeNode<K,V> x, f = first;
// 将当前节点构建出来
first = x = new TreeNode<K,V>(h, k, v, f, xp);
// 因为当前的TreeBin除了红黑树还维护这一个双向链表,维护双向链表的操作
if (f != null)
f.prev = x;
// 维护红黑树操作
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 如果如节点是黑色的,当前节点红色即可,说明现在插入的节点没有影响红黑树的平衡
if (!xp.red)
x.red = true;
else {
// 说明插入的节点是黑色的
// 加锁操作
lockRoot();
try {
// 自平衡一波。
root = balanceInsertion(root, x);
} finally {
// 释放锁操作
unlockRoot();
}
}
break;
}
}
// 检查一波红黑树结构
assert checkInvariants(root);
// 代表插入了新节点
return null;
}
# 4.6 TreeBin的锁操作
TreeBin的锁操作,没有基于AQS,仅仅是对一个变量的CAS操作和一些业务判断实现的。
每次读线程操作,对lockState+4。
写线程操作,对lockState + 1,如果读操作占用着线程,就先+2,waiter是当前线程,并挂起当前线程
// TreeBin的锁操作
// 如果说有读线程在读取红黑树的数据,这时,写线程要阻塞(做平衡前)
// 如果有写线程正在操作红黑树(做平衡),读线程不会阻塞,会读取双向链表
// 读读不会阻塞!
static final class TreeBin<K,V> extends Node<K,V> {
// waiter:等待获取写锁的线程
volatile Thread waiter;
// lockState:当前TreeBin的锁状态
volatile int lockState;
// 对锁状态进行运算的值
// 有线程拿着写锁
static final int WRITER = 1;
// 有写线程,再等待获取写锁
static final int WAITER = 2;
// 读线程,在红黑树中检索时,需要先对lockState + READER
// 这个只会在读操作中遇到
static final int READER = 4;
// 加锁-写锁
private final void lockRoot() {
// 将lockState从0设置为1,代表拿到写锁成功
if (!U.compareAndSwapInt(this, LOCKSTATE, 0, WRITER))
// 如果写锁没拿到,执行contendedLock
contendedLock();
}
// 释放写锁
private final void unlockRoot() {
lockState = 0;
}
// 写线程没有拿到写锁,执行当前方法
private final void contendedLock() {
// 是否有线程正在等待
boolean waiting = false;
// 死循环,s是lockState的临时变量
for (int s;;) {
//
// lockState & 11111101 ,只要结果为0,说明当前写锁,和读锁都没线程获取
if (((s = lockState) & ~WAITER) == 0) {
// CAS一波,尝试将lockState再次修改为1,
if (U.compareAndSwapInt(this, LOCKSTATE, s, WRITER)) {
// 成功拿到锁资源,并判断是否在waiting
if (waiting)
// 如果当前线程挂起过,直接将之前等待的线程资源设置为null
waiter = null;
return;
}
}
// 有读操作在占用资源
// lockState & 00000010,代表当前没有写操作挂起等待。
else if ((s & WAITER) == 0) {
// 基于CAS,将LOCKSTATE的第二位设置为1
if (U.compareAndSwapInt(this, LOCKSTATE, s, s | WAITER)) {
// 如果成功,代表当前线程可以waiting等待了
waiting = true;
waiter = Thread.currentThread();
}
}
else if (waiting)
// 挂起当前线程!会由写操作唤醒
LockSupport.park(this);
}
}
}
# 4.7 transfer迁移数据
首先红黑结构的数据迁移是基于双向链表封装的数据。
如果高低位的长度小于等于6,封装为链表迁移到新数组
如果高低位的长度大于6,依然封装为红黑树迁移到新数组
// 红黑树的迁移操作单独拿出来,TreeBin中不但有红黑树,还有双向链表,迁移的过程是基于双向链表迁移
TreeBin<K,V> t = (TreeBin<K,V>)f;
// lo,hi扩容后要放到新数组的高低位的链表
TreeNode<K,V> lo = null, loTail = null;
TreeNode<K,V> hi = null, hiTail = null;
// lc,hc在记录高低位数据的长度
int lc = 0, hc = 0;
// 遍历TreeBin中的双向链表
for (Node<K,V> e = t.first; e != null; e = e.next) {
int h = e.hash;
TreeNode<K,V> p = new TreeNode<K,V>(h, e.key, e.val, null, null);
// 与老数组长度做&运算,基于结果确定需要存放到低位还是高位
if ((h & n) == 0) {
if ((p.prev = loTail) == null)
lo = p;
else
loTail.next = p;
loTail = p;
// 低位长度++
++lc;
}
else {
if ((p.prev = hiTail) == null)
hi = p;
else
hiTail.next = p;
hiTail = p;
// 高位长度++
++hc;
}
}
// 封装低位节点,如果低位节点的长度小于等于6,转回成链表。 如果长度大于6,需要重新封装红黑树
ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K,V>(lo) : t;
// 封装高位节点
hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K,V>(hi) : t;
// 低位数据设置到新数组
setTabAt(nextTab, i, ln);
// 高位数据设置到新数组
setTabAt(nextTab, i + n, hn);
// 当前位置数据迁移完毕,设置上fwd
setTabAt(tab, i, fwd);
// 开启前一个节点的数据迁移
advance = true;
# 五、查询数据
# 5.1 get方法-查询数据的入口
在查询数据时,会先判断当前key对应的value,是否在数组上。
其次会判断当前位置是否属于特殊情况:数据被迁移、位置被占用、红黑树结构
最后判断链表上是否有对应的数据。
找到返回指定的value,找不到返回null即可
// 基于key查询value
public V get(Object key) {
// tab:数组, e:查询指定位置的节点 n:数组长度
Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek;
// 基于传入的key,计算hash值
int h = spread(key.hashCode());
// 数组不为null,数组上得有数据,拿到指定位置的数组上的数据
if ((tab = table) != null && (n = tab.length) > 0 && (e = tabAt(tab, (n - 1) & h)) != null) {
// 数组上数据恩地hash值,是否和查询条件key的hash一样
if ((eh = e.hash) == h) {
// key的==或者equals是否一致,如果一致,数组上就是要查询的数据
if ((ek = e.key) == key || (ek != null && key.equals(ek)))
return e.val;
}
// 如果数组上的数据的hash为负数,有特殊情况,
else if (eh < 0)
// 三种情况,数据迁移走了,节点位置被占,红黑树
return (p = e.find(h, key)) != null ? p.val : null;
// 肯定走链表操作
while ((e = e.next) != null) {
// 如果hash值一致,并且key的==或者equals一致,返回当前链表位置的数据
if (e.hash == h && ((ek = e.key) == key || (ek != null && key.equals(ek))))
return e.val;
}
}
// 如果上述三个流程都没有知道指定key对应的value,那就是key不存在,返回null即可
return null;
}
# 5.2 ForwardingNode的find方法
在查询数据时,如果发现已经扩容了,去新数组上查询数据
在数组和链表上正常找key对应的value
可能依然存在特殊情况:
- 再次是fwd,说明当前线程可能没有获取到CPU时间片,导致CHM再次触发扩容,重新走当前方法
- 可能是被占用或者是红黑树,再次走另外两种find方法的逻辑
// 在查询数据时,发现当前桶位置已经放置了fwd,代表已经被迁移到了新数组
Node<K,V> find(int h, Object k) {
// key:get(key) h:key的hash tab:新数组
outer: for (Node<K,V>[] tab = nextTable;;) {
// n:新数组长度, e:新数组上定位的位置上的数组
Node<K,V> e; int n;
if (k == null || tab == null || (n = tab.length) == 0 || (e = tabAt(tab, (n - 1) & h)) == null)
return null;
// 开始在新数组中走逻辑
for (;;) {
// eh:新数组位置的数据的hash
int eh; K ek;
// 判断hash是否一致,如果一致,再判断==或者equals。
if ((eh = e.hash) == h && ((ek = e.key) == k || (ek != null && k.equals(ek))))
// 在新数组找到了数据
return e;
// 发现到了新数组,hash值又小于0
if (eh < 0) {
// 套娃,发现刚刚在扩容,到了新数组,发现又扩容
if (e instanceof ForwardingNode) {
// 再次重新走最外层循环,拿到最新的nextTable
tab = ((ForwardingNode<K,V>)e).nextTable;
continue outer;
}
else
// 占了,红黑树
return e.find(h, k);
}
// 说明不在数组上,往下走链表
if ((e = e.next) == null)
// 进来说明链表没找到,返回null
return null;
}
}
}
# 5.3 ReservationNode的find方法
没什么说的,直接返回null
因为当前桶位置被占用的话,说明数据还没放到当前位置,当前位置可以理解为就是null
Node<K,V> find(int h, Object k) {
return null;
}
# 5.4 TreeBin的find方法
在红黑树中执行find方法后,会有两个情况
- 如果有线程在持有写锁或者等待获取写锁,当前查询就要在双向链表中锁检索
- 如果没有线程持有写锁或者等待获取写锁,完全可以对lockState + 4,然后去红黑树中检索,并且在检索完毕后,需要对lockState - 4,再判断是否需要唤醒等待写锁的线程
// 在红黑树中检索数据
final Node<K,V> find(int h, Object k) {
// 非空判断
if (k != null) {
// e:Treebin中的双向链表,
for (Node<K,V> e = first; e != null; ) {
int s; K ek;
// s:TreeBin的锁状态
// 00000010
// 00000001
if (((s = lockState) & (WAITER|WRITER)) != 0) {
// 如果进来if,说明要么有写线程在等待获取写锁,要么是由写线程持有者写锁
// 如果出现这个情况,他会去双向链表查询数据
if (e.hash == h && ((ek = e.key) == k || (ek != null && k.equals(ek))))
return e;
e = e.next;
}
// 说明没有线程等待写锁或者持有写锁,将lockState + 4,代表当前读线程可以去红黑树中检索数据
else if (U.compareAndSwapInt(this, LOCKSTATE, s, s + READER)) {
TreeNode<K,V> r, p;
try {
// 基于findTreeNode在红黑树中检索数据
p = ((r = root) == null ? null : r.findTreeNode(h, k, null));
} finally {
Thread w;
// 会对lockState - 4,读线程拿到数据了,释放读锁
// 可以确认,如果-完4,等于WAITER,说明有写线程可能在等待,判断waiter是否为null
if (U.getAndAddInt(this, LOCKSTATE, -READER) == (READER|WAITER) && (w = waiter) != null)
// 当前我是最后一个在红黑树中检索的线程,同时有线程在等待持有写锁,唤醒等待的写线程
LockSupport.unpark(w);
}
return p;
}
}
}
return null;
}
# 5.6 TreeNode的findTreeNode方法
红黑树的检索方式,套路很简单,及时基于hash值,来决定去找左子树还有右子数。
如果hash值一致,判断是否 == 、equals,满足就说明找到数据
如果hash值一致,并不是找的数据,基于compare方式,再次决定找左子树还是右子数,知道找到当前节点的子节点为null,停住。
// 红黑树中的检索方法
final TreeNode<K,V> findTreeNode(int h, Object k, Class<?> kc) {
if (k != null) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk; TreeNode<K,V> q;
// 声明左子树和右子数
TreeNode<K,V> pl = p.left, pr = p.right;
// 直接比较hash值,来决决定走左子树还是右子数
if ((ph = p.hash) > h)
p = pl;
else if (ph < h)
p = pr;
// 判断当前的子树是否和查询的k == 或者equals,直接返回
else if ((pk = p.key) == k || (pk != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
// 递归继续往底层找
else if ((q = pr.findTreeNode(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
}
return null;
}
# 六、ConcurrentHashMap其他方法
# 6.1 compute方法
修改ConcurrentHashMap中指定key的value时,一般会选择先get出来,然后再拿到原value值,基于原value值做一些修改,最后再存放到咱们ConcurrentHashMap
public static void main(String[] args) {
ConcurrentHashMap<String,Integer> map = new ConcurrentHashMap();
map.put("key",1);
// 修改key对应的value,追加上1
// 之前的操作方式
Integer oldValue = (Integer) map.get("key");
Integer newValue = oldValue + 1;
map.put("key",newValue);
System.out.println(map);
// 现在的操作方式
map.compute("key",(key,computeOldValue) -> {
if(computeOldValue == null){
computeOldValue = 0;
}
return computeOldValue + 1;
});
System.out.println(map);
}
# 6.2 compute方法源码分析
整个流程和putVal方法很类似,但是内部涉及到了占位的情况RESERVED
整个compute方法和putVal的区别就是,compute方法的value需要计算,如果key存在,基于oldValue计算出新结果,如果key不存在,直接基于oldValue为null的情况,去计算新的value。
// compute 方法
public V compute(K key, BiFunction<? super K, ? super V, ? extends V> remappingFunction) {
if (key == null || remappingFunction == null)
throw new NullPointerException();
// 计算key的hash
int h = spread(key.hashCode());
V val = null;
int delta = 0;
int binCount = 0;
// 初始化,桶上赋值,链表插入值,红黑树插入值
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
// 初始化
if (tab == null || (n = tab.length) == 0)
tab = initTable();
// 桶上赋值
else if ((f = tabAt(tab, i = (n - 1) & h)) == null) {
// 数组指定的索引位置是没有数据,当前数据必然要放到数组上。
// 因为value需要计算得到,计算的时间不可估计,所以这里并没有通过CAS的方式处理并发操作,直接添加临时占用节点,
// 并占用当前临时节点的锁资源。
Node<K,V> r = new ReservationNode<K,V>();
synchronized (r) {
// 以CAS的方式将数据放上去
if (casTabAt(tab, i, null, r)) {
binCount = 1;
Node<K,V> node = null;
try {
// 如果ReservationNode临时Node存放成功,直接开始计算value
if ((val = remappingFunction.apply(key, null)) != null) {
delta = 1;
// 将计算的value和传入的key封装成一个新Node,通过CAS存储到当前数组上
node = new Node<K,V>(h, key, val, null);
}
} finally {
setTabAt(tab, i, node);
}
}
}
if (binCount != 0)
break;
}
else {
// 省略部分代码。主要是针对在链表上的替换、添加,以及在红黑树上的替换、添加
}
}
if (delta != 0)
addCount((long)delta, binCount);
return val;
}
# 6.3 computeIfPresent、computeIfAbsent、compute区别
compute的BUG,如果在计算结果的函数中,又涉及到了当前的key,会造成死锁问题。
public static void main(String[] args) {
ConcurrentHashMap<String,Integer> map = new ConcurrentHashMap();
map.compute("key",(k,v) -> {
return map.compute("key",(key,value) -> {
return 1111;
});
});
System.out.println(map);
}
computeIfPresent和computeIfAbsent其实就是将compute方法拆开成了两个方法
compute会在key不存在时,正常存放结果,如果key存在,就基于oldValue计算newValue
computeIfPresent:要求key在map中必须存在,需要基于oldValue计算newValue
computeIfAbsent:要求key在map中不能存在,必须为null,才会基于函数得到value存储进去
computeIfPresent:
// 如果key存在,才执行修改操作
public V computeIfPresent(K key, BiFunction<? super K, ? super V, ? extends V> remappingFunction) {
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
if (tab == null || (n = tab.length) == 0)
tab = initTable();
// 如果key不存在,什么事都不做~
else if ((f = tabAt(tab, i = (n - 1) & h)) == null)
break;
else {
synchronized (f) {
if (tabAt(tab, i) == f) {
if (fh >= 0) {
binCount = 1;
for (Node<K,V> e = f, pred = null;; ++binCount) {
K ek;
// 如果查看到有 == 或者equals的key,就直接修改即可
if (e.hash == h &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
val = remappingFunction.apply(key, e.val);
if (val != null)
e.val = val;
else {
delta = -1;
Node<K,V> en = e.next;
if (pred != null)
pred.next = en;
else
setTabAt(tab, i, en);
}
break;
}
pred = e;
// 走完链表,还是没找到指定数据,直接break;
if ((e = e.next) == null)
break;
}
}
// 省略部分代码
return val;
}
computeIfAbsent核心位置源码:
// key必须不存在才会执行添加操作
public V computeIfAbsent(K key, Function<? super K, ? extends V> mappingFunction) {
for (Node<K,V>[] tab = table;;) {
else if ((f = tabAt(tab, i = (n - 1) & h)) == null) {
// 如果key不存在,正常添加;
Node<K,V> r = new ReservationNode<K,V>();
synchronized (r) {
if (casTabAt(tab, i, null, r)) {
binCount = 1;
Node<K,V> node = null;
try {
if ((val = mappingFunction.apply(key)) != null)
node = new Node<K,V>(h, key, val, null);
} finally {
setTabAt(tab, i, node);
}
}
}
}
else {
boolean added = false;
synchronized (f) {
if (tabAt(tab, i) == f) {
if (fh >= 0) {
binCount = 1;
for (Node<K,V> e = f;; ++binCount) {
K ek; V ev;
// 如果key存在,直接break;
if (e.hash == h &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
val = e.val;
break;
}
// 如果没有找到一样的key,计算value结果接口
Node<K,V> pred = e;
if ((e = e.next) == null) {
if ((val = mappingFunction.apply(key)) != null) {
added = true;
pred.next = new Node<K,V>(h, key, val, null);
}
break;
}
}
}
// 省略部分代码
return val;
}
# 6.4 replace方法详解
涉及到类似CAS的操作,需要将ConcurrentHashMap的value从val1改为val2的场景就可以使用replace实现。
replace内部要求key必须存在,替换value值之前,要先比较oldValue,只有oldValue一致时,才会完成替换操作。
// replace方法调用的replaceNode方法, value:newValue, cv:oldValue
final V replaceNode(Object key, V value, Object cv) {
int hash = spread(key.hashCode());
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
// 在数组没有初始化时,或者key不存在时,什么都不干。
if (tab == null || (n = tab.length) == 0 ||
(f = tabAt(tab, i = (n - 1) & hash)) == null)
break;
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
V oldVal = null;
boolean validated = false;
synchronized (f) {
if (tabAt(tab, i) == f) {
if (fh >= 0) {
validated = true;
for (Node<K,V> e = f, pred = null;;) {
K ek;
// 找到key一致的Node了。
if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) {
// 拿到当前节点的原值。
V ev = e.val;
// 拿oldValue和原值做比较,如果一致,
if (cv == null || cv == ev || (ev != null && cv.equals(ev))) {
// 可以开始替换
oldVal = ev;
if (value != null)
e.val = value;
else if (pred != null)
pred.next = e.next;
else
setTabAt(tab, i, e.next);
}
break;
}
pred = e;
if ((e = e.next) == null)
break;
}
}
else if (f instanceof TreeBin) {
validated = true;
TreeBin<K,V> t = (TreeBin<K,V>)f;
TreeNode<K,V> r, p;
if ((r = t.root) != null &&
(p = r.findTreeNode(hash, key, null)) != null) {
V pv = p.val;
if (cv == null || cv == pv ||
(pv != null && cv.equals(pv))) {
oldVal = pv;
if (value != null)
p.val = value;
else if (t.removeTreeNode(p))
setTabAt(tab, i, untreeify(t.first));
}
}
}
}
}
if (validated) {
if (oldVal != null) {
if (value == null)
addCount(-1L, -1);
return oldVal;
}
break;
}
}
}
return null;
}
# 6.5 merge方法详解
merge(key,value,Function<oldValue,value>);
在使用merge时,有三种情况可能发生:
- 如果key不存在,就跟put(key,value);
- 如果key存在,就可以基于Function计算,得到最终结果
- 结果不为null,将key对应的value,替换为Function的结果
- 结果为null,删除当前key
分析merge源码
public V merge(K key, V value, BiFunction<? super V, ? super V, ? extends V> remappingFunction) {
if (key == null || value == null || remappingFunction == null) throw new NullPointerException();
int h = spread(key.hashCode());
V val = null;
int delta = 0;
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
if (tab == null || (n = tab.length) == 0)
tab = initTable();
// key不存在,直接执行正常的添加操作,将value作为值,添加到hashMap
else if ((f = tabAt(tab, i = (n - 1) & h)) == null) {
if (casTabAt(tab, i, null, new Node<K,V>(h, key, value, null))) {
delta = 1;
val = value;
break;
}
}
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
synchronized (f) {
if (tabAt(tab, i) == f) {
if (fh >= 0) {
binCount = 1;
for (Node<K,V> e = f, pred = null;; ++binCount) {
K ek;
// 判断链表中,有当前的key
if (e.hash == h && ((ek = e.key) == key || (ek != null && key.equals(ek)))) {
// 基于函数,计算value
val = remappingFunction.apply(e.val, value);
// 如果计算的value不为null,正常替换
if (val != null)
e.val = val;
// 计算的value是null,直接让上一个指针指向我的next,绕过当前节点
else {
delta = -1;
Node<K,V> en = e.next;
if (pred != null)
pred.next = en;
else
setTabAt(tab, i, en);
}
break;
}
pred = e;
if ((e = e.next) == null) {
delta = 1;
val = value;
pred.next =
new Node<K,V>(h, key, val, null);
break;
}
}
}
else if (f instanceof TreeBin) {
binCount = 2;
TreeBin<K,V> t = (TreeBin<K,V>)f;
TreeNode<K,V> r = t.root;
TreeNode<K,V> p = (r == null) ? null :
r.findTreeNode(h, key, null);
val = (p == null) ? value :
remappingFunction.apply(p.val, value);
if (val != null) {
if (p != null)
p.val = val;
else {
delta = 1;
t.putTreeVal(h, key, val);
}
}
else if (p != null) {
delta = -1;
if (t.removeTreeNode(p))
setTabAt(tab, i, untreeify(t.first));
}
}
}
}
if (binCount != 0) {
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i);
break;
}
}
}
if (delta != 0)
addCount((long)delta, binCount);
return val;
}
